Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD và ΔECD có
góc ADB=góc EDC
góc ABD=góc ECD
=>ΔABD đồng dạng với ΔECD
b: AD là phân giác
=>DB/AB=DC/AC
=>DB/8=DC/12
=>DB/2=DC/3=(DB+DC)/(2+3)=15/5=3
=>DB=6cm; DC=9cm

Xét ΔBAC có
AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{12}=\dfrac{CD}{20}\)
mà BD+CD=28cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{12}=\dfrac{CD}{20}=\dfrac{BD+CD}{12+20}=\dfrac{28}{32}=\dfrac{7}{8}\)
Do đó: BD=10,5cm; CD=17,5cm
Xét ΔBAC có
DE//AB
nên \(\dfrac{DE}{AB}=\dfrac{CD}{BC}\)
\(\Leftrightarrow DE=\dfrac{17.5}{28}\cdot12=7.5\left(cm\right)\)

a: Xét ΔABD và ΔECD có
\(\widehat{ADB}=\widehat{EDC}\)
\(\widehat{ABD}=\widehat{ECD}\)
Do đó; ΔABD\(\sim\)ΔECD
b: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/8=DC/12
=>DB/2=DC/3
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{2}=\dfrac{DC}{3}=\dfrac{DB+DC}{2+3}=\dfrac{15}{5}=3\)
Do đó: DB=6cm; DC=9cm

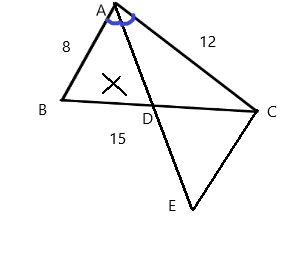
a) Vì AB//CE (gt)
=> BAD = CED (so le trong)
Xét tam giác ABD và tam giác ECD có
BAD = CED (cmt)
ADB = EDC (đối đỉnh)
=> Tam giác ABD đồng dạng với tam giác ECD
b) Đặt BD là x, ta có:
CD = BC - BD = 15 - x
Xét tam giác ABC có AD là đường phân giác (gt) nên
=> BD/DC = AB/AC (Tính chất đường phân giác trong tam giác)
Thay số: x/15 - x = 8/12
=> 12x = 8(15 - x)
(=) 12x = 120 - 8x
(=) 20x = 120
(=) x = 6
=> BD = 6
=> CD = BC - BD = 15 - 6 = 9 cm
