Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do ban lop 7 nen bài này mình làm theo cách lớp 7 nhé.Hinh ban tu ve nhe
a)Xet tam giac AMC va tam giac CMB co
MA=MC
MB=ME
goc AME=goc CMB(doi dinh)
=> tam giac AMC = tam giac CMB
=>AE=BC,goc EAM=goc MCB
=> AE=BC,AE//BC
b) Câu này để phải là trên tia đối của tia NC
Lam tuong tu cau a
=> AF=BC,AF//BC
DO AF=BC,AE=BC=> AE=AF
Do AF//BC,AE//BC=> A,F,E thang hang
=> A la trung diem cua EF
c)Tren tia doi nua NM lay D sao cho NM=ND
Do tam giac ANM=tam giac BND (c.g.c)
=>goc MAN=goc NBD,AM=BD
=>AM=BD,AM//BD(hay MC)
ma AM=MC
=>BD=MC,BD//MC
=>MD=BC,MD//BC(Tinh chat doan chan)
=> MN=1/2BC,MN//BC

a) Xét tam giác AME và tam giác BMC, có:
góc AME = góc BMC ( đối đỉnh)
EM = MC ( giải thiết )
AM= MB ( M là trung điểm của AB )
\(\Rightarrow\) TAm giác AME = tam giác BMC ( c-g-c)
\(\Rightarrow\)góc AEM = góc BCM ( hai góc tương ứng)
\(\Rightarrow AE\)//\(BC\) ( đpcm)

a: Xét tứ giác AEBC có
M là trung điểm của AB
M là trung điểm của EC
Do đó: AEBC là hình bình hành
Suy ra: AE=BC
b: Xét tứ giác ABCF có
N là trung điểm của AC
N là trung điểm của BF
Do đó: ABCF là hình bình hành
Suy ra: AF=BC
mà AE=BC
nên AE=FA
a: Xét tứ giác AEBC có
M là trung điểm của AB
M là trung điểm của EC
Do đó: AEBC là hình bình hành
Suy ra: AE=BC
b: Xét tứ giác ABCF có
N là trung điểm của AC
N là trung điểm của BF
Do đó: ABCF là hình bình hành
Suy ra: AF=BC
mà AE=BC
nên AE=FA

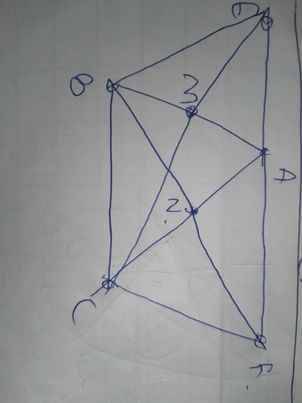
a: Xét ΔAME và ΔBMC có
MA=MB
\(\widehat{AME}=\widehat{BMC}\)(hai góc đối đỉnh)
ME=MC
Do đó: ΔAME=ΔBMC
b: Xét ΔAFN và ΔCBN có
NA=NC
\(\widehat{ANF}=\widehat{CNB}\)(hai góc đối đỉnh)
NF=NB
Do đó: ΔAFN=ΔCBN
c: ΔAME=ΔBMC
=>\(\widehat{MAE}=\widehat{MBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
d: ΔAME=ΔBMC
=>AE=BC
ΔANF=ΔCNB
=>\(\widehat{NAF}=\widehat{NCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//BC
ΔANF=ΔCNB
=>AF=CB
Ta có: AF=CB
AE=BC
Do đó: AE=AF
Ta có: AE//BC
AF//BC
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng
mà AE=AF
nên A là trung điểm của EF

Xét tứ giác AEBC có
M là trung điểm của đường chéo AB
M là trung điểm của đường chéo CE
Do đó: AEBC là hình bình hành
Suy ra: AE//BC và AE=BC(1)
Xét tứ giác ABCF có
N là trung điểm của đường chéo AC
N là trung điểm của đường chéo BF
Do đó: ABCF là hình bình hành
Suy ra: AF//BC và AF=BC(2)
Từ (1) và (2) suy ra AE=AF
Ta có: AE//BC
AF//BC
mà AE và AF có điểm chung là A
nên E,A,F thẳng hàng
mà AE=AF
nên A là trung điểm của EF

xét tam giác ame và tam giác bmc
me=mc (gt)
góc ema= góc bmc (đối đỉnh)
am=bm( m là trung điểm của ab)
=> tam giác ame= tam giác bmc(c.g.c)
=> góc eam= góc cbm ( 2 cạnh tương ứng)
mà góc eam và góc cbm SLT
=>ae //bc
xét tam giác afn và tam giác cbn
fn=bn (gt)
góc an f= góc bnc (đ đ)
an=cn ( n là trung điểm của ac)
=> tam giác a fn= tam giác cbn (c.g.c)
=> a f=cb (2 cạnh t ung)
mà ae=cb (tam giác ame= tam giác bmc)
=>a f= ae (=cb)
=> a là trung điểm của e f
 Trang 2 nek, z là hết mờ hen^^
Trang 2 nek, z là hết mờ hen^^ Trang 1 nek
Trang 1 nek
Xét tam giác ABC, có: N là trung điểm AC
}
M là trung điểm AB
=> MN là đườg trung bình tam giác ABC
=> MN//BC (1)
Chứng minh tương tự ta có : MN là đường trung bình tam giác AEC
=> MN //AE (2)
{
MN=1/2AE (3)
Từ (1) và (2) => AE//BC (đpcm)
b) Xét tam giác ABF, có : M là trung điểm AB
}
N là trung điểm BF (NF=NB)
=> MN là đường trung bình tam giác ABF
=> MN =1/2 AF (4)
Từ (3) và (4) => AE = AF
Mà A nằm giữa E và F
=> A là trung điểm của EF.
Vậy .....................