Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C E F I 1 2 1
Vì điểm I cách đều ba cạnh của tam giác ABC và nằm trong tam giác nên I là giao điểm của ba đường phân giác của tam giác ABC, tức BI, CI lần lượt là tia phân giác của góc B và góc C. Do EF // BC nên \(\widehat{B_1}=\widehat{I_1}\) (hai góc so le trong), suy ra \(\widehat{I_1}=\widehat{B_2}\). Vậy tam giác EBI cân tại E, tức là EI = EB. Tương tự ta có FI = FC.
Vậy EF = EI + IF = BE + CF.

Vì AD và BE là 2 đường trung tuyến của ΔABC cắt nhau tại G nên theo tính chất đường trung tuyến, ta có: AG = 2/3 AD

Áp dụng kết quả bài 64 chương II sách Bài tập toán 7 vào ΔABC và ΔAGB ta có:
DE // AB và DE = 1/2 AB (1)
IK // AB và IK = 1/2 AB (2)
Từ (1) và (2) suy ra:
DE // IK và DE = IK.

A B C M N P I H O
a) MP // AC => ^MPB=^CAB; ^PMB=^ACB. Mà ^CAB=^ACB=600
=> ^MPB=^PMB=600 => Tam giác BPM là tam giác đều (đpcm).
b) Tam giác BPM là tam giác đều (cmt) => PM=BP
Ta có: PM//AN; M//AP => PM=AN (Tính chất đoạn chắn)
=> BP=AN.
Tam giác ABC đều và O là trọng tâm nên ta có: ^OBA=^OAC=300 hay ^OBP=^OAN và OB=OA
Xét tam giác OAN và tam giác OBP: BP=AN; OA=OB; ^OAN=^OBP
=> Tam giác OAN= Tam giác OBP (đpcm)
c) Tam giác AIP=Tam giác MIN (g.c.g) => IP=IN hay I là trung điểm của NP
Tam giác OAN=Tam giác OBP (cmt) => ON=OP => O nằm trên trung trực của NP (1)
HP=HN => H nằm trên trung trực của NP (2)
Từ (1) và (2) kết hợp với I là trung điểm của NP => H;I;O thẳng hàng (đpcm).

a: Xét tứ giác BFED có
ED//BF
FE//BD
Do đó: BFED là hình bình hành
Xét ΔABC có
D là trung điểm của BC
DE//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
E là trung điểm của AC
EF//CB
Do đó: F là trung điểm của AB
Xét ΔCDE và ΔEFA có
CD=EF
DE=FA
CE=EA
Do đó: ΔCDE=ΔEFA
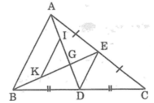
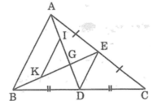
b: Gọi ΔABC có F là trung điểm của AB,E là trung điểm của AC
Trên tia FE lấy điểm E sao cho E là trung điểm của FK
Xét tứ giác AFCK có
E là trung điểm của AC
E là trung điểm của FK
Do đó: AFCK là hình bình hành
Suy ra: AF//KC và KC=AF
hay KC//FB và KC=FB
Xét tứ giác BFKC có
KC//FB
KC=FB
Do đó: BFKC là hình bình hành
Suy ra: FE//BC(ĐPCM)
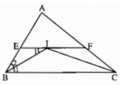
Vì điểm I cách đều ba cạnh của tam giác ABC và nằm trong tam giác nên I là giao điểm của ba đường phân giác của tam giác ABC, tức là BI, CI lần lượt là tia phân giác của góc N và góc C. Do EF // BC nên ∠B1= ∠I1(so le trong), suy ra ∠I2 = ∠B2 .
Suy ra: BI, CI lần lượt là tia phân giác của góc B và góc C.
Do EF // BC nên ∠B1 = ∠BIE (so le trong).
Lại có: ∠B1 = ∠B2 ( vì BI là tia phân giác của góc B )
Suy ra: ∠B2 = ∠BIE
Vậy EF = EI + IF = BE + CF.