Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

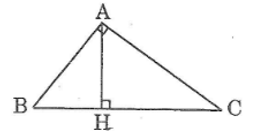
\(\Delta ABH\sim\Delta CAH\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{C_{ABC}}{C_{CAH}}=\dfrac{30}{40}=\dfrac{3}{4}\)
=> \(\dfrac{AB^2}{9}=\dfrac{AC^2}{16}=\dfrac{BC^2}{25}\)
\(\Rightarrow\dfrac{AB}{3}=\dfrac{AC}{4}=\dfrac{BC}{5}\\\)
=> \(\dfrac{AB}{BC}=\dfrac{3}{5}\)
\(\Delta ABH\sim\Delta CBA\)
\(\Rightarrow\dfrac{C_{ABH}}{C_{ABC}}=\dfrac{AB}{BC}\)
=> Chu vi tam giác ABC là 30 . 5 : 3 = 50
Gọi a, b, c lần lượt là chu vi của các tam giác ABC, ABH, ACH.
Ta có: b = 30cm, c = 40cm
Xét hai tam giác vuông AHB và CHA, ta có:

Gọi a, b, c lần lượt là chu vi của các tam giác ABC, ABH, ACH.
Ta có: b = 30cm, c = 40cm
Xét hai tam giác vuông AHB và CHA, ta có:


Tam giác ABH và CAH vuông và có ^BAH=^C (cùng phụ với góc B)
Nên Tam giác ABH và CAH đồng dạng (g-g) =>AB/AC = k (tỷ số đồng dạng)
Mà C(ABH) / C(CAH) = k (tỷ số chu vi bằng tỷ số đồng dạng)
suy ra 30/40 = k hay k = 3/4.
do đó AB/AC = 3/4 hay AB/3 = AC/4 = t
=> AB = 3t; AC = 4t Theo Pitago ta tính được BC = 5t.
Vậy chu vi tam giác ABC là AB+AC+BC = 3t+4t+5t = 12t.


300 cm