Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)

Xét \(\Delta ABC\) vuông tại A có \(AB^2+AC^2=BC^2\) (định lý Pytago)
\(\Rightarrow BC^2=12^2+16^2=20^2\Rightarrow BC=20\).
Theo tính chất đường phân giác trong tam giác ABC ta có:
\(\dfrac{BD}{AB}=\dfrac{CD}{AC}=\dfrac{CD+BD}{AC+AB}=\dfrac{BC}{AC+AB}=\dfrac{20}{12+16}=\dfrac{5}{7}\Rightarrow BD=\dfrac{60}{7};CD=\dfrac{80}{7}\).
Ta có \(AH.BC=AB.AC\left(=2S_{ABC}\right)\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{48}{5}\).
Từ đó \(BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-\left(\dfrac{48}{5}\right)^2}=\dfrac{36}{5}\).
Suy ra \(HD=\left|BD-BH\right|=\left|\dfrac{48}{5}-\dfrac{36}{5}\right|=\dfrac{12}{5}\).
\(AD=\sqrt{AH^2+HD^2}=\dfrac{12\sqrt{17}}{5}\).

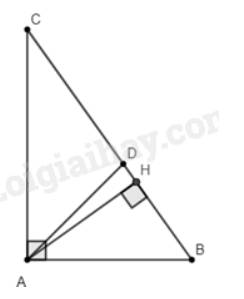
a)
Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\)
\( \Leftrightarrow {3^2} + {4^2} = B{C^2}\)
\( \Leftrightarrow B{C^2} = 25\)
\( \Rightarrow BC = 5cm\)
Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 5 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{5 - BD}} = \frac{3}{4} \Leftrightarrow 4.BD = 3.\left( {5 - BD} \right) \Rightarrow 4.BD = 15 - 3.BD\)
\( \Leftrightarrow 4BD + 3BD = 15 \Leftrightarrow 7BD = 15 \Rightarrow BD = \frac{{15}}{7}\)
\( \Rightarrow DC = 5 - \frac{{15}}{7} = \frac{{20}}{7}\)
Vậy \(BC = 5cm;BD = \frac{{15}}{7}cm;DC = \frac{{20}}{7}cm\).
b) Diện tích tam giác \(ABC\) vuông tại \(A\) là:
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.4.3 = 6\left( {c{m^2}} \right)\)
Mặt khác \({S_{ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.AH.5 = 6\)
\( \Rightarrow AH = \frac{{6.2}}{5} = 2,4cm\).
Xét tam giác \(AHB\) vuông tại \(H\) ta có:
\(A{H^2} + H{B^2} = A{B^2}\)
\( \Leftrightarrow H{B^2} = A{B^2} - A{H^2}\)
\( \Leftrightarrow H{B^2} = {3^2} - 2,{4^2}\)
\( \Leftrightarrow H{B^2} = 3,24\)
\( \Rightarrow HB = 1,8cm\)
\(HD = BD - BH = \frac{{15}}{7} - 1,8 = \frac{{12}}{7}cm\).
Xét tam giác \(AHD\) vuông tại \(H\) ta có:
\(A{H^2} + H{D^2} = A{D^2}\)
\( \Leftrightarrow A{D^2} = {\left( {\frac{{12}}{7}} \right)^2} + 2,{4^2}\)
\( \Leftrightarrow A{D^2} = \frac{{144}}{{49}} + \frac{{144}}{{25}}\)
\( \Rightarrow AD \approx 2,95cm\)
Vậy \(AH = 2,4cm;HD = \frac{{12}}{7}cm;AD = 2,95cm\).

Xét ΔABC có AD là đường phân giác
nên AB/AC=BD/CD=3/4
=>BH/CH=9/16
=>BH=6,3
=>CH=11,2
=>AH=8,4

a) Áp dụng định lý Pi-ta-go vào \(\Delta\)vuông ABC có :
\(AB^2+AC^2=BC^2\Leftrightarrow BC=20\left(cm\right)\)
Do AD là phân giác \(\widehat{A}\)theo tính chất đường phân giác , ta có :
\(\frac{BD}{CD}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}\)
\(\Rightarrow\frac{BD}{BD+CD}=\frac{3}{3+4}\Rightarrow\frac{BD}{BC}=\frac{3}{7}\)
\(\Rightarrow BD=\frac{3}{7}BC=\frac{60}{7}\)
\(\Rightarrow DC=BC-BD=\frac{80}{7}\)
b) AH là đường cao \(\Delta\)vuông ABC nên :
\(S_{\Delta ABC}=\frac{AH.BC}{2}=\frac{AB.AC}{2}\)
\(\Rightarrow AH=\frac{AB.C}{BC}=\frac{48}{5}\left(cm\right)\)
Ta có :
\(BH^2=AB^2-AH^2\Rightarrow BH=\frac{36}{5}\left(cm\right)\)
\(\Rightarrow DH=BD=BH=\frac{48}{35}\left(cm\right)\)
\(AD^2=DH^2+AH^2\Rightarrow AD=\frac{48\sqrt{2}}{7}\left(cm\right)\)

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/AB
=>BA^2=BH*BC
b: \(AB=\sqrt{9\cdot25}=15\left(cm\right)\)
AC=căn 16*25=20(cm)
S=15*20/2=150cm2
c: AD/DC=HA/HC=12/16=3/4
Xét ΔABC có AD là đường phân giác
nên AB/AC=BD/CD
=>AB/AC=3/4
=>HB/HC=9/16
=>\(HB=17.5\cdot\dfrac{9}{25}=6.3\)
=>HC=11,2
=>AH=8,4