Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vẽ hình lỗi nên ko vẽ được
a) xét \(\Delta BAM\)VÀ\(\Delta CDM\)CÓ
AM=MD(GT)
\(\widehat{BMA}=\widehat{CMD}\left(Đ^2\right)\)
BM=CM (GT)
=>\(\Delta BAM\)=\(\Delta CDM\)(C-G-C)
=> ab=cd( hai cạnh tương ứng )
\(\Rightarrow\widehat{ABM}=\widehat{DCM}\)HAY\(\widehat{ABC}=\widehat{DCB}\)( hai góc trương ứng)
MÀ HAI GÓC NÀY Ở VỊ TRÍ SO LE TRONG = NHAU
\(\Rightarrow AB//CD\left(đpcm\right)\)
xét \(\Delta BDM\)VÀ\(\Delta CAM\)CÓ
\(BM=CM\left(GT\right)\)
\(\widehat{BMD}=\widehat{CMA}\left(Đ^2\right)\)
\(DM=AM\left(GT\right)\)
=>\(\Delta BDM\)=\(\Delta CAM\)(C-G-C)
=> BD=AC ( HAI CẠNH TƯƠNG ỨNG )
\(\Rightarrow\widehat{MBD}=\widehat{MCA}\)HAY\(\widehat{CBD}=\widehat{BCA}\)( HAI GÓC TƯƠNG ỨNG )
HAI GÓC NÀY Ở VỊ TRÍ S SOLE TRONG BẰNG NHAU
=>AC//BD
B) đề sai

a.
Xét \(\Delta AMB\) và \(\Delta DMC\) ; có :
\(MA=MD\left(gt\right)\\ \widehat{AMB}=\widehat{DMC}\left(đ^2\right)\\ MB=MC\\ \Rightarrow\Delta AMB=\Delta DMC\left(c-g-c\right)\\ \Rightarrow AB=CD;\widehat{MAB}=\widehat{MDC}\\ \widehat{MAB}=\widehat{MDC}\)
=> AB // CD
TT : AC// BD ; AC=BD
b.
Có vấn đề chỗ BF cắt BC tại K ; !!
coi lại đề

a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )

a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDClà hình bình hành
SUy ra: AB//CD; AB=CD; AD//BC và AD=BC
b: Xét ΔABD có
BM là đường trung tuyến
AE là đường trung tuyến
BM cắt AE tại I
Do đó; I là trọng tâm của ΔABD
Xét ΔACD có
DF là đường trung tuyến
CM là đường trung tuyến
DF cắt CM tại K
Do đó: K là trọng tâm của ΔACD

Mình làm câu đầu tiên nhé :)
a) Xét tam giác ABM và tam giác DMC có :
BM = CM ( gt )
\(\widehat{AMB}=\widehat{DMC}\)
AM = DM ( gt )
\(\Rightarrow\)\(\Delta AMB=\Delta DMC\left(c-g-c\right)\)
\(\Rightarrow\)\(\widehat{BAM}=\widehat{DCM}\)( 2 góc tương ứng bằng nhau )
Mà 2 góc này ở vị trí so le trong nên suy ra AB // CD


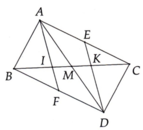
a)
*Chứng minh AB//CD và AB=CD
Xét ΔAMB và ΔDMC có
AM=DM(gt)
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
BM=CM(AM là đường trung tuyến ứng với cạnh BC trong ΔABC)
Do đó: ΔAMB=ΔDMC(c-g-c)
⇒\(\widehat{ABM}=\widehat{DCM}\)(hai góc tương ứng)
mà \(\widehat{ABM}\) và \(\widehat{DCM}\) là hai góc ở vị trí so le trong
nên AB//CD(dấu hiệu nhận biết hai đường thẳng song song)(đpcm1)
Ta có: ΔABM=ΔDCM(cmt)
⇒AB=CD(hai cạnh tương ứng)(đpcm2)
*Chứng minh AC//BD và AC=BD
Xét ΔAMC và ΔDMB có
AM=DM(gt)
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
CM=BM(AM là đường trung tuyến ứng với cạnh BC của ΔABC)
Do đó: ΔAMC=ΔDMB(c-g-c)
⇒\(\widehat{MAC}=\widehat{MDB}\)(hai góc tương ứng)
mà \(\widehat{MAC}\) và \(\widehat{MDB}\) là hai góc ở vị trí so le trong
nên AC//BD(dấu hiệu nhận biết hai đường thẳng song song)(đpcm3)
Ta có: ΔAMC=ΔDMB(cmt)
⇒AC=BD(hai cạnh tương ứng)(đpcm4)