Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì I đối xứng với H qua AC => \(\widehat{AIC}=\widehat{AHC}=90^o\)=>\(\widehat{AIC}+\widehat{AHC}=180^o\)=> AICH nội tiếp
b, Vì I đối xứng với H qua qua AC=> AI=AH
Vì I đối xứng với K qua qua AB=>AK=AH=> AI=AK
c,\(\widehat{KHB}=\widehat{ECB}\)vì cùng phụ với góc ABC (AB vuông góc với KH)
=> KH//CE. Mà CE vuông góc với AB=> CE vuông góc với AB => góc CEA =90 độ
=> Góc CEA= góc CHA =90 độ => AEHC nội tiếp. Mà AICH nội tiếp (theo a)
=> 5 điểm A,E,H,C,I cùng thuộc 1 đường tròn

a: Ta có: H và I đối xứng nhau qua AC
nên AH=AI; CI=CH
Xét ΔAHC và ΔAIC có
AH=AI
HC=IC
AC chung
Do đó: ΔAHC=ΔAIC
SUy ra: \(\widehat{AHC}=\widehat{AIC}=90^0\)
=>AHCI là tứ giác nội tiếp
b: Ta có: H và K đối xứng nhau qua AB
nên AH=AK
=>AK=AI

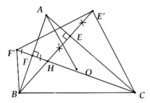
a, ∆CHE' cân tại C => C E ' H ^ = C H E ' ^
DBHF' cân tại B => B F ' H ^ = B H F ' ^
Mà => C H E ' ^ = B H F ' ^ (đối đỉnh)
=> C E ' H ^ = B F ' H ^
=> Tứ giác BCE'F' nội tiếp đường tròn tâm (O)
b, Có B F C ' ^ = B E ' C ^ = C H E ' ^ = C A B ^
Vậy A, F', E' cùng chắn BC dưới góc bằng nhau
=> 5 điểm B, F', A, E', C cùng thuộc một đường tròn tâm (O)
c, AF' = AE' (=AH) => AO là trung trực của EF => AO ^ E'F'. DHE'F' có EF là đường trung bình => EF//E'F'
=> AO ^ FE
d, A F H ^ = A E H ^ = 90 0 => AFHE nội tiếp đường tròn đường kính AH. Trong (O): Kẻ đường kính AD, lấy I trung điểm BC
=> OI = 1 2 AH, BC cố định => OI không đổi
=> Độ dài AH không đổi
=> Bán kính đường tròn ngoại tiếp ∆AEF không đổi