Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài làm
Bài 2:
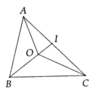
a) Xét tam giác AOI có:
Theo bất đẳng thức của tam giác có:
OA < IA + IO
=> OA < IA + BI - OB
=> OA + OB < AI + IB (đpcm )

Bạn tự vẽ hình nha![]()
a.
Xét tam giác COA vuông tại C và tam giác DOB vuông tại D có:
OA = OB (gt)
AOB là góc chung
=> Tam giác COA = Tam giác DOB (cạnh huyền - góc nhọn)
b.
OA = OB (gt)
=> Tam giác OAB cân tại O
OAC + CAB = OAB
OBD + DBA = OBA
mà OAC = OBD (tam giác AOC = tam giác BOD)
OAB = OBA (tam giác OAB cân tại O)
=> CAB = DBA
=> Tam giác IAB cân tại I
c.
Tam giác CIB vuông tại C có:
IC < IB (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà IA = IB (tam giác IBA cân tại I)
=> IC < IA
d.
Tam giác OAB cân tại O
=> \(OBA=\frac{180-AOB}{2}=\frac{180}{2}-\frac{AOB}{2}=90-\frac{AOB}{2}\)
Tam giác CAB vuông tại C có:
IAB + OBA = 90
IAB = 90 - OBA = \(90-\left(90-\frac{AOB}{2}\right)=90-90+\frac{AOB}{2}=\frac{AOB}{2}\)
=> IAB = 1/2 AOB
Chúc bạn học tốt![]()

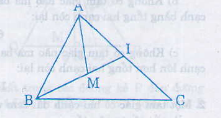
a) Ta có M nằm trong \(\Delta ABM.\)
=> \(A,M,I\) không thẳng hàng.
Theo bất đẳng thức tam giác với \(\Delta AMI\) có:
\(AM< MI+IA\left(1\right).\)
b) Cộng vào hai vế của (1) với \(MB\) ta được:
\(AM+MB< MB+MI+IA\)
Mà \(MB+MI=IB.\)
=> \(AM+MB< BI+IA.\)
c) Ta có 3 điểm \(B,I,C\) không thẳng hàng.
Theo bất đẳng thức tam giác với \(\Delta BIC\) có:
\(BI< IC+BC.\) (2)
d) Cộng vào hai vế của (2) với \(IA\) ta được:
\(BI+IA< IA+IC+BC\)
Mà \(IA+IC=AC.\)
=> \(BI+IA< AC+BC.\)
e) Vì \(\left\{{}\begin{matrix}AM+MB< BI+IA\left(cmt\right)\\BI+IA< AC+BC\left(cmt\right)\end{matrix}\right.\)
=> \(AM+MB< AC+BC.\)
Chúc bạn học tốt!

 tham khảo nha
tham khảo nha
Trời ơi chứng minh nhiều thế ! XyGalaXy