Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).
A E F C D B
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt)
(theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ∆ABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật vừa là hình thoi).

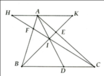
Qua A kẻ đường thẳng song song với BC, cắt CF, BE lần lượt tại H, K
AH // BC nên theo định lí Talet ta có: A F F B = A H B C
AK //BC nên theo định lí Talet ta có: A E E C = A K B C
Suy ra A F F B + A E E C = A H B C + A K B C = H K C B hay A F F B + A E E C = K H B C (1)
Lại có: AH // DC nên theo định lí Talet ta có: A I I D = A H D C
AK // BD nên theo định lí Talet ta có: A I I D = A K B D
Do đó A I I D = A H D C = A K B D (2)
Theo tính chất dãy tỉ số bằng nhau A H D C = A K B D = A I + A K D C + B D = H K B C (3)
Từ (2) và (3) suy ra A I I D = H K B C (4)
Từ (1) và (4) suy ra A F F B + A E E C = A I I D
Đáp án B