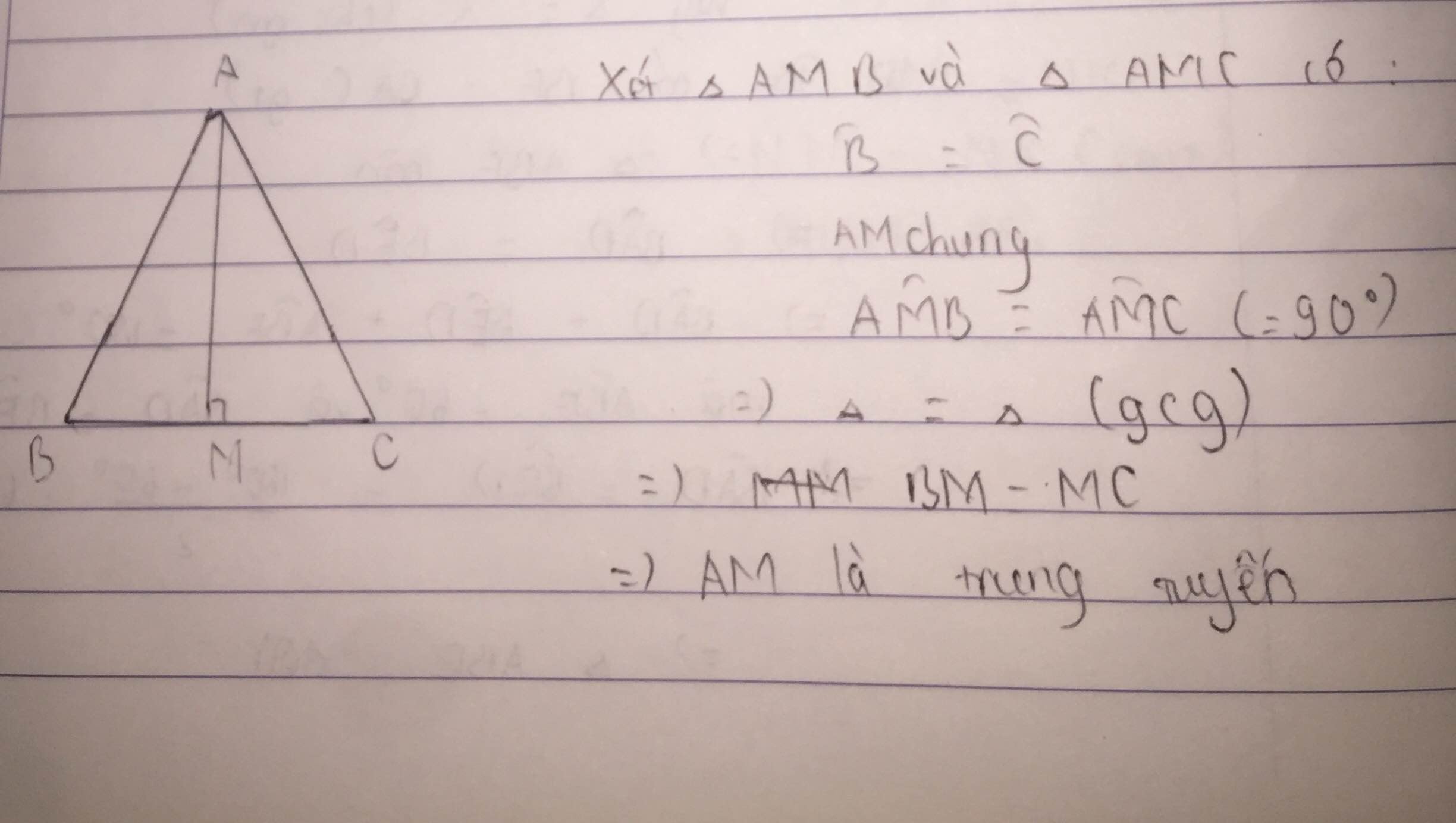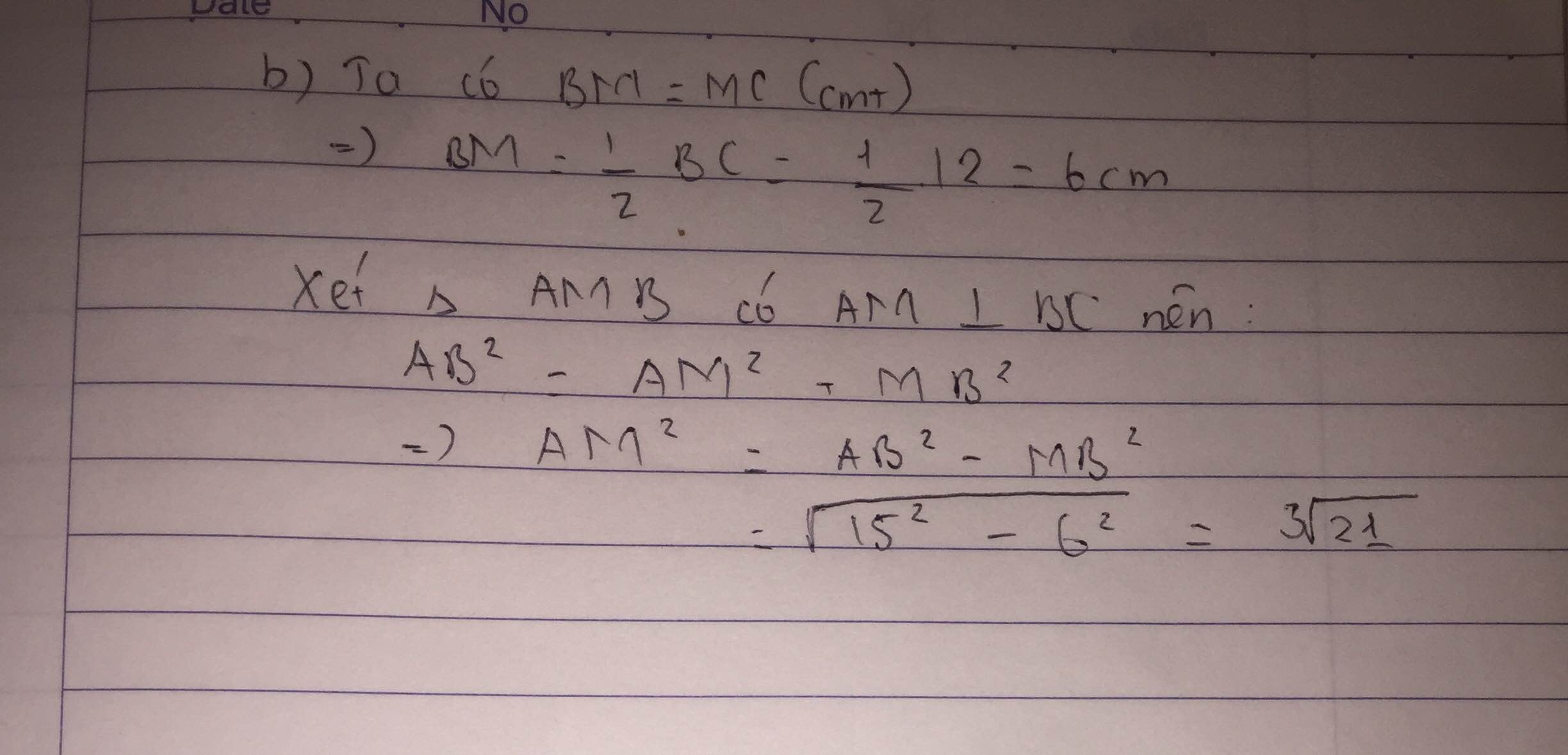TT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TA
15 tháng 6 2021
Áp dụng định lí Pytago:
`BC^2=AB^2+AC^2`
`<=>BC^2=3^2+4^2`
`<=>BC=5(cm)`
AM là đường trung tuyến của `\DeltaABC`
`=> AM = (BC)/2 = 5/2 (cm)`
20 tháng 5 2022
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔABC cân tại A
mà AM là trung tuyến
nên AM là đường cao
BC=12cm nên BM=6cm
=>AM=8(cm)
c: I cách đều ba cạnh nên I là giao điểm của ba đường phân giác
=>AI là phân giác của góc BAC
mà AM là phân giác của góc BC
nên A,I,M thẳng hàng
NT
3
19 tháng 3 2020
tam giác ABC đều ; AM là trung tuyến
=> AM đồng thời là đường cao
=> AM _|_ BC
=> tam giác AMC vuông tại M
=> AM^2 + CM^2 = AC^2 (Pytago)
M là trung điểm của BC => CM = BC/2 = 6/2 = 3
AC = 6
=> AM^2 + 3^2 = 6^2
=> AM^2 = 27
=> AM = \(\sqrt{27}\) do AM > 0
PT
1
CM
10 tháng 3 2017
Chú ý AM là đường cao, từ đó dùng Định lý Pytago tính được AM = 12 cm.