Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

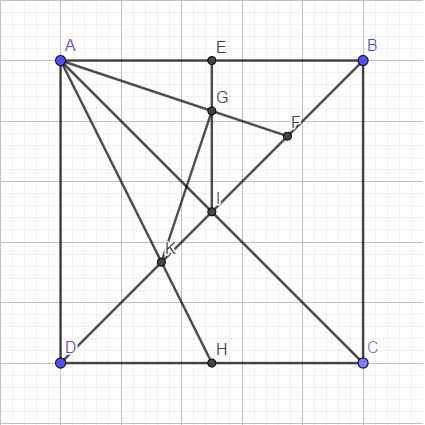
Đặt tên điểm như hình vẽ bên dưới
Ta có: F là trung điểm BI \(\Rightarrow\overrightarrow{AF}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AI}\right)\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AF}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AI}\right)=\dfrac{1}{3}\left(\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AC}\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{6}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\)
\(\overrightarrow{AH}=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AK}=\dfrac{2}{3}\overrightarrow{AH}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}\)
\(\overrightarrow{GK}=\overrightarrow{GA}+\overrightarrow{AK}=-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{6}\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}=-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AG}.\overrightarrow{GK}=\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\right)\left(-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\right)=-\dfrac{1}{12}AB^2+\dfrac{1}{12}AD^2=0\)
\(\Rightarrow AG\perp GK\)
\(\left\{{}\begin{matrix}\overrightarrow{GA}=\left(a+\dfrac{1}{3};b\right)\\\overrightarrow{KG}=\left(0;\dfrac{5}{3}\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{GA}.\overrightarrow{KG}=\left(a+\dfrac{1}{3}\right).0+\dfrac{5}{3}b=0\Rightarrow b=0\)
Mặt khác: \(AG^2-GK^2=\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\right)^2-\left(-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\right)^2=0\)
\(\Rightarrow AG^2=GK^2\Rightarrow\left(a+\dfrac{1}{3}\right)^2=\left(\dfrac{5}{3}\right)^2\Rightarrow a=-2\)

phép quay thì phải là góc quay chứ bạn.
Còn tỉ số k=2/3 thì là phép vị tự nha bạn
Lấy A' trên GA sao cho GA'=2/3GA
Lấy B' trên GB sao cho GB'=2/3GB
Lấy C' trên GC sao cho GC'=2/3GC
=>ảnh của ΔABC qua \(V_{\left(G;\dfrac{2}{3}\right)}\) là ΔA'B'C'

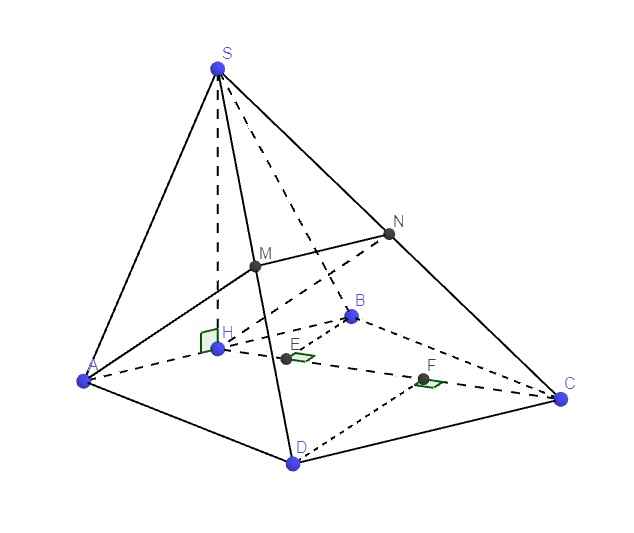
Tam giác SAB đều \(\Rightarrow SH\perp AB\)
Mà \(\left\{{}\begin{matrix}AB=\left(SAB\right)\cap\left(ABCD\right)\\\left(SAB\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABCD\right)\)
Gọi N là trung điểm SC \(\Rightarrow MN\) là đường trung bình tam giác SCD
\(\Rightarrow\left\{{}\begin{matrix}MN||CD\\MN=\dfrac{1}{2}CD\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}MN||AH\\MN=AH\end{matrix}\right.\) \(\Rightarrow AMNH\) là hbh
\(\Rightarrow AM||HN\Rightarrow AM||\left(SHC\right)\)
\(\Rightarrow d\left(AM;SC\right)=d\left(AM;\left(SHC\right)\right)=d\left(A;\left(SHC\right)\right)\)
Mặt khác H là trung điểm AB \(\Rightarrow d\left(A;\left(SHC\right)\right)=d\left(B;\left(SHC\right)\right)\)
Từ B kẻ \(BE\perp HC\Rightarrow BE\perp\left(SHC\right)\) (do \(SH\perp BE\))
\(\Rightarrow BE=d\left(B;\left(SHC\right)\right)\)
Hệ thức lượng: \(BE=\dfrac{BH.BC}{CH}=\dfrac{BH.BC}{\sqrt{BH^2+BC^2}}=\dfrac{a\sqrt{5}}{5}\)
b.
Từ D kẻ \(DF\perp HC\Rightarrow DF\perp\left(SHC\right)\) (do \(SH\perp DF\))
\(\Rightarrow DF=d\left(D;\left(SHC\right)\right)\)
\(DF=DC.cos\widehat{FDC}=DC.cos\widehat{BCH}=\dfrac{DC.BC}{CH}=\dfrac{DC.BC}{\sqrt{BC^2+BH^2}}=\dfrac{2a\sqrt{5}}{5}\)

S A C B H
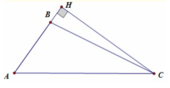
Kẻ đường cao AH của \(\Delta SAB\)
Ta có: SA\(\perp\)( ABC ) = > SA\(\perp\)BC
mà AB \(\perp\)BC ( tam giác ABC vuông tại B )
=> BC \(\perp\)(SAB ) => BC \(\perp\)AH lại có: AH \(\perp\)SB ( theo cách vẽ đường cao)
=> AH \(\perp\)(SBC )
=> d ( A; (SBC )) = AH
Xét \(\Delta\)SAB vuông tại A có AH là đường cao
=> \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{SA^2}=\frac{1}{a^2}+\frac{1}{4a^2}=\frac{5}{4a^2}\Rightarrow AH=\frac{2\sqrt{5}}{5}\)
Vậy d ( A; (SBC )) = AH = \(\frac{2\sqrt{5}}{5}\)

[Số cách chọn 4 em sao cho thuộc không quá 2 trong 3 lớp] = [Số cách chọn 4 em trong 12 em] - [số cách chọn mà mỗi lớp có ít nhất 1 em]
Mà:
[Số cách chọn 4 em trong 12 em] = \(C^4_{12}=\frac{12!}{4!\left(12-4\right)!}=495\)
[số cách chọn mà mỗi lớp có ít nhất 1 em] = [Số cách chọn lớp A có 2 hs, lớp B, C mỗi lớp có 1 hs] + [Số cách chọn lớp B có 2 hs, lớp A, C mỗi lớp có 1 hs] + [Số cách chọn lớp C có 2 hs, lớp A, B mỗi lớp có 1 hs]
= \(C^2_5.C^1_4.C^1_3+C^1_5.C^2_4.C^1_3+C^1_5.C^1_4.C^2_3\)
= 120 + 90 + 60
= 270
Vậy [Số cách chọn 4 em sao cho thuộc không quá 2 trong 3 lớp] = 495 - 270 =....

Vì 147=3*7*7
189=3*3*3*7
168=3*2*2*7
=> ƯC(147;189;168)=3.7=21
Vậy mỗi hàng có 21 em học sinh.
Khối 6 xếp được: 147/21=7 hàng
Khối 7 xếp được: 189/21=9 hàng
Khối 8 xếp được: 168/21=8 hàng
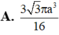
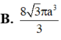
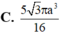
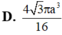


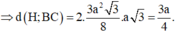
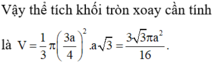


Đáp án A.