Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác đều ANC có đường cao AH.
Do tam giác ANC là tam giác đều nên đường cao đồng thời là đường trung tuyến.
Ta có A H = A C . sin A C H ^ = a . sin 60 0 = a 3 2
G là trọng tâm tam giác nên: A G = 2 3 . A H = 2 3 . a 3 2 = a 3 3
Đáp án D

Nếu G là trong tâm tam giác ABC thì
G A → + G B → + G C → = 0 → ⇔ A G → + B G → + C G → = 0 → ⇔ A G → + B G → + C G → = 0 → = 0
Đáp án C

\(T=\overrightarrow{GA}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)+\overrightarrow{GB}.\overrightarrow{CA}+\overrightarrow{GC}.\overrightarrow{AB}\)
\(=\overrightarrow{AB}\left(\overrightarrow{GC}-\overrightarrow{GA}\right)+\overrightarrow{AC}\left(\overrightarrow{GA}-\overrightarrow{GB}\right)\)
\(=\overrightarrow{AB}\left(\overrightarrow{GC}+\overrightarrow{AG}\right)+\overrightarrow{AC}\left(\overrightarrow{GA}+\overrightarrow{BG}\right)\)
\(=\overrightarrow{AB}.\overrightarrow{AC}+\overrightarrow{AC}.\overrightarrow{BA}\)
\(=0\)

Kẻ \(\overrightarrow{AH}=\overrightarrow{GC}\)
ΔABC đều có G là trọng tâm
nên G là tâm đường tròn nội tiếp ΔABC
=>AG,CG,BG lần lượt là phân giác của góc \(\widehat{BAC};\widehat{ACB};\widehat{ABC}\)
ΔABC đều
=>\(\widehat{BAC}=\widehat{ACB}=\widehat{ABC}=60^0\)
AG là phân giác của góc BAC
=>\(\widehat{BAG}=\widehat{CAG}=\dfrac{1}{2}\cdot\widehat{BAC}=\dfrac{1}{2}\cdot60^0=30^0\)
CG là phân giác của góc ACB
=>\(\widehat{ACG}=\widehat{BCG}=\dfrac{1}{2}\cdot\widehat{ACB}=30^0\)
Xét ΔGAC có \(\widehat{AGC}+\widehat{GAC}+\widehat{GCA}=180^0\)
=>\(\widehat{AGC}+30^0+30^0=180^0\)
=>\(\widehat{AGC}=120^0\)
\(\overrightarrow{AH}=\overrightarrow{GC}\)
=>AH//GC và AH=GC
Xét tứ giác AHCG có
AH//CG
AH=CG
Do đó: AHCG là hình bình hành
=>\(\widehat{GAH}+\widehat{AGC}=180^0\)
=>\(\widehat{GAH}=180^0-120^0=60^0\)
ΔABC đều có G là trọng tâm
nên \(AG=CG=BG=\dfrac{a\sqrt{3}}{3}=\dfrac{2\sqrt{3}\cdot\sqrt{3}}{3}=2\)
\(\overrightarrow{AB}-\overrightarrow{GC}=\overrightarrow{AB}-\overrightarrow{AH}=\overrightarrow{AB}+\overrightarrow{HA}=\overrightarrow{HB}\)
\(\widehat{BAH}=\widehat{BAG}+\widehat{GAH}=30^0+60^0=90^0\)
=>ΔABH vuông tại A
AH=CG
mà 2
nên AH=2
ΔABH vuông tại A
=>\(BH^2=AB^2+AH^2\)
=>\(BH^2=\left(2\sqrt{3}\right)^2+2^2=16\)
=>BH=4
=>\(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|=\left|\overrightarrow{HB}\right|=HB=4\)
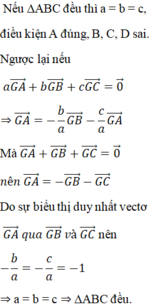
Lời giải:
Kéo dài $GC$ cắt $AB$ tại $H$.
\(\Rightarrow \overrightarrow {GC}=\frac{2}{3}\overrightarrow{HC}=\frac{2}{3}(\overrightarrow{HA}+\overrightarrow{AC})\)
Do tam giác $ABC$ đều nên $CH$ là trung trực của $AB$
\(\Rightarrow \overrightarrow{HA}=\frac{1}{2}\overrightarrow{BA}\)
Vậy:
\(\overrightarrow{AB}-\overrightarrow{GC}=\overrightarrow{AB}-\frac{2}{3}(\frac{1}{2}\overrightarrow{BA}+\overrightarrow{AC})\)
\(=\overrightarrow{AB}-\frac{1}{3}\overrightarrow{BA}-\frac{2}{3}\overrightarrow{AC}=\frac{4}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{AC}=\frac{2}{3}(\overrightarrow{AB}+\overrightarrow{AB}-\overrightarrow{AC})=\frac{2}{3}(\overrightarrow{AB}+\overrightarrow{CB})\)
Trên tia đối của $BC$ lấy $D$ sao cho \(BD=BC=a\)
\(\Rightarrow \overrightarrow{CB}=\overrightarrow{BD}\)
\(\Rightarrow \overrightarrow{AB}-\overrightarrow{GC}=\frac{2}{3}(\overrightarrow{AB}+\overrightarrow{BD})=\frac{2}{3}\overrightarrow{AD}\)
\(\Rightarrow |\overrightarrow{AB}-\overrightarrow{GC}|=\frac{2}{3}|\overrightarrow{AD}|\)
Xét tam giác $ADC$ có trung truyến $AB$ bằng một nửa cạnh huyền $DC$ nên là tam giác vuông tại $A$
\(\Rightarrow AD=\sqrt{DC^2-AC^2}=\sqrt{(2a)^2-a^2}=\sqrt{3}a\)
Do đó \(|\overrightarrow{AB}-\overrightarrow{GC}|=\frac{2}{3}.\sqrt{3}a=\frac{2\sqrt{3}a}{3}\)
cảm ơn nhìu ạ :)