Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

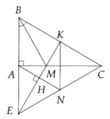
a, xét tam giác ABM và tam giác KBM có: AB=BK, BM chung, góc ABM= góc KBM
suy ra 2 tam giác trên bằng nhau
hok tốt
tu ve hinh :
xet tamgiac ABM va tamgiac KBM co : MB chung
goc ABM = goc MBK do BM la phan giac cua goc ABC (gt)
AB = AK (gt)
=> tammgiac ABM = tamgiac KBM (c - g - c)

a, xét tam giác ABM và tam giác KBM có :BM chung
góc ABM = góc KBM do BM là pg của góc ABC (gt)
AB = BK (gt)
=> tam giác ABM = tma giác KBM (c-g-c)
b, tam giác ABM = tam giác KBM (Câu a)
=> góc MAB = góc MKB (đn)
góc MAB = 90
=> góc MKB = 90
xét tam giác EMA và tam giác CMK có : góc CMK = góc EMA (đối đỉnh)
MA = MK do tam giác ABM = tam giác KBM (câu a)
góc MAE = góc MKC = 90
=> tam giác EMA = tam giác CMK (cgv-gnk)
=> MA = MC (đn)
=> tam giác EMC cân tại M (đn)
c, tam giác ABC vuông tại A (gt) => góc ABC + góc ACB = 90 (đl)
góc ACB = 30 (gt)
=> góc ABC = 60 (1)
BA = BK (gt)
AE = CK do tam giác MEA = tam giác MCK (câu b)
AE + AB = BE
CK + KB = BC
=> BE = BC
=> tam giác BEC cân tại B (đn) và (1)
=> tam giác BEC đều (dh)

a, xét tam giác ABM và tam giác KBM có :
BM chung
góc ABM = góc KBM do BM là pg của góc ABC (gt)
AB = BK (gt)
=> tam giác ABM = tam giác KBM (c-g-c)
b, tam giác ABM = tam giác KBM (Câu a)
=> góc MAB = góc MKB (đn)
góc MAB = 90
=> góc MKB = 90
xét tam giác EMA và tam giác CMK có :
góc CMK = góc EMA (đối đỉnh)
MA = MK do tam giác ABM = tam giác KBM (câu a)
góc MAE = góc MKC = 90
=> tam giác EMA = tam giác CMK (cgv-gnk)
=> MA = MC (đn)
=> tam giác EMC cân tại M (đn)
c, tam giác ABC vuông tại A (gt) => góc ABC + góc ACB = 90 (đl)
góc ACB = 30 (gt)
=> góc ABC = 60 (1)
BA = BK (gt)
AE = CK
do tam giác MEA = tam giác MCK (câu b)
AE + AB = BE
CK + KB = BC
=> BE = BC
=> tam giác BEC cân tại B (đn) và (1)
=> tam giác BEC đều (dh)
:)

Tham khảo
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC
refer
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC