Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C F D E
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE ( gt ) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu \(\Delta ABC\) vuông tại A thì AEDF là hình chữ nhật ( vì là hình bình hành có một góc vuông )
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông ( vì vừa là hình chữ nhật, vừa là hình thoi )

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

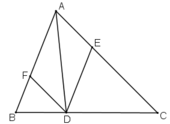
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

c , Xét hình bình hành AEDF có
góc A = 90
=> Hình bình hành AEDF là Hình chữ nhật ( dhnb)
Ta có Hình bình hành AEDF là hình chữ nhật (cmt)
=> AD = EF ( t/c )
AD ngắn nhất => D là chân đường vuông góc từ điểm A đến đoạn thẳng BC ( đường vuông góc là đường ngắn nhất)
Vậy để đoạn thẳng EF có độ dài nhỏ nhất thì điểm D phải là chân đường vuông góc từ A đến cạnh BC
d, Trên các cạnh AB, AC lần lượt lấy M,N là trung điểm của chúng.
A,B,C cố định \(\Rightarrow\) M,N cố định \(\Rightarrow\) đoạn MN cố định (MN// BC)
\(\Delta ABD\) có: \(\left\{{}\begin{matrix}AM=MB\left(gt\right)\\AI=ID\left(gt\right)\end{matrix}\right.\) \(\Rightarrow\) IM là đường trung bình
\(\Rightarrow\) MI// BD hay MI// BC (1)
C/m tương tự: IN là đường trung bình của \(\Delta ACD\)
\(\Rightarrow\) NI// DC hay NI // BC (2)
Từ (1) và (2), theo tiên đề Ơ-clít, qua một điểm nằm ngoài đường thẳng chỉ có một đường thẳng song song với nó
\(\Rightarrow\) I, M,N thẳng hàng \(\Rightarrow\) I nằm trên MN
Vậy khi điểm D di chuyển trên cạnh BC thì trung điểm I của AD di chuyển trên đường trung bình của \(\Delta ABC\)
P/s: Lớp 8 phải làm dài dòng phết, lớp 9 làm quỹ tích cơ -.-

a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).
A E F C D B
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt)
(theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ∆ABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật vừa là hình thoi).

a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).
F thuộc AC nha