Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

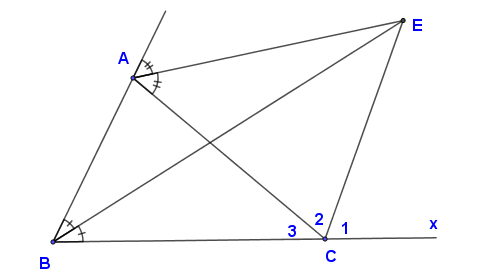
▶▸ Ta có: BEBE là tia phân giác góc BB (giả thiết)
AEAE là tia phân giác góc ngoài tại đỉnh AA (giả thiết)
⇒⇒ CECE là tia phân giác góc ngoài tại đỉnh CC (định lý bổ sung)
▶▸ Trên tia đối của tia CBCB vẽ tia CxCx
Khi đó ACxˆACx^ và C3ˆC3^ là hai góc kề bù
⇒⇒ ACxˆ=180o−C3ˆ=180o−30o=150oACx^=180o−C3^=180o−30o=150o
Vì CECE là tia phân giác của ACxˆACx^ ⇒⇒ C1ˆ=C2ˆ=ACxˆ2=150o2=75oC1^=C2^=ACx^2=150o2=75o
⇒⇒ BCEˆ=C3ˆ+C2ˆ=30o+75o=105oBCE^=C3^+C2^=30o+75o=105o

1, Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(tổng 3 góc tam giác)
\(\Leftrightarrow\widehat{C}+90^o+\widehat{C}=180^o\)
\(\Leftrightarrow2\widehat{C}=90^o\)
\(\Leftrightarrow\widehat{C}=45^o\)
\(\Rightarrow\widehat{A}=\widehat{C}+10=55^o\)
\(\Rightarrow\widehat{B}=180^o-\widehat{A}-\widehat{C}=180^o-55^o-45^o=80^o\)
2,
A B C M 1 1
Vì tam giác ABC vuông tại A
=> ^B + ^C = 90o
Vì BM là phân giác ^ABC
=>^B1 = \(\frac{\widehat{ABC}}{2}\)
Tương tự ^C1 = \(\frac{\widehat{ACB}}{2}\)
\(\Rightarrow\widehat{B_1}+\widehat{C_1}=\frac{\widehat{ABC}+\widehat{ACB}}{2}=\frac{90^o}{2}=45^o\)
Theo tổng 3 góc trong tam giác \(\widehat{BMC}=180^o-\widehat{B_1}-\widehat{C_1}=180^o-45^o=135^o\)

Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.