Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)
góc BDA=180°-105°=75°
góc ABD= 90°-75°=15°
=> góc ABC=15°.2=30°
góc ACB=90°-30°=60°
2)
góc BIC=(180°- góc BAC)/2=130°
=> góc ABC=130°.2-180°=260-180°=80°
1/ góc BDC = 105* => góc ADB = 75* ( hai góc kề bù )
=> góc DBA = 90*-75*=15*
=> góc B = 2. góc DBA = 2. 15 = 30* ( phân giác BD)
=> góc C = 90* - 30*= 60*

Hướng dẫn:
a) ∆KIL có ˆII^ = 620
nên ˆIKL+ˆILKIKL^+ILK^ = 1180
Vì KO và LO là phân giác ˆIKLIKL^, ˆILKILK^
nên ˆOKL+ˆOLKOKL^+OLK^= 1212(ˆIKL+ˆILKIKL^+ILK^)
=> ˆOKL+ˆOLKOKL^+OLK^ = 1212 1180
ˆOKL+ˆOLKOKL^+OLK^ = 590
∆KOL có ˆOKL+ˆOLKOKL^+OLK^ = 590
nên ˆKOLKOL^ = 1800 – 590 = 1210

c) Vì O là giao điểm của hai đường phân giác của ˆKK^ và ˆLL^ nên O cách đều ba cạnh của tam giác IKL
a, Áp dụng định lí tổng 3 góc trong ΔIKL, ta có:
∠I + ∠IKL + ∠ILK= 180 độ
⇒ ∠IKL + ∠ILK= 180 độ - ∠I
OK, OL là phân giác của các góc K, L nên:
∠OKL= 1/2∠IKL, ∠OLK= 1/2∠ILK
⇒ ∠OKL + ∠OLK= 1/2 (∠IKL + ∠ILK)
= 1/2 . (180 độ - ∠I)
Áp dụng định lí tổng 3 góc trong ΔOKL có:
∠ KOL + ∠OKL + ∠OLK = 180 độ
⇒ ∠KOL= 180 độ - (∠OKL + ∠OLK)
= 180 độ - 180- ∠I / 2= 180 + ∠I/2
Mà ∠I= 62 độ nên:
∠KOL= 180 +62/2= 121 độ
b, Ta có: 3 đường phân giác trong tam giác đồng quy.
Mà 2 đường phân giác KO, LO cắt nhau tại O
⇒ OI là tia phân giác của ∠KIL
⇒ ∠KIO= 1/2 ∠KIL= 1/2. 62 độ= 31 độ
c, O là giao điểm 3 đường phân giác của ΔIKL. Áp dụng định lí 3 đường phân giác
Vậy O cách đều 3 cạnh của ΔIKL


 Bài 1. Cho tam giác ABC cân tại A có Â = 80o
Bài 1. Cho tam giác ABC cân tại A có Â = 80o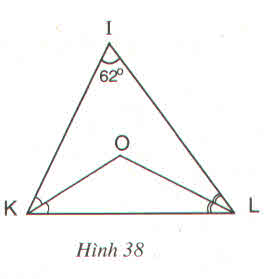
Bạn bổ sung đề đi bạn: Số đo của góc B và góc C là bao nhiêu???
ko có chỉ có A thôi