Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó:ΔHBA\(\sim\)ΔABC
2: \(BC=\sqrt{AB^2+AC^2}=15\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=7.2\left(cm\right)\)

a) xét tam giác ABH và tam giác CBA
có góc B chung
góc AGB= góc BAC=90
=>tam giác ABH đồng dạng tam giác CBA
=>\(\dfrac{AB}{CB}=\dfrac{AH}{CA}\)
b) áp dụng định lý pytago có
AB2+AC2=BC2
Thay AB=8;AC=6
=>BC=10
Theo câu a)có:\(\dfrac{AB}{CB}=\dfrac{AH}{CA}\)
thay số \(\dfrac{8}{10}=\dfrac{AH}{6}\)
=>AH=4,8

Xét ΔFHB vuông tại F và ΔEHC vuông tại E có
\(\widehat{FHB}=\widehat{EHC}\)
Do đó: ΔFHB\(\sim\)ΔEHC
Suy ra: HF/HE=HB/HC
hay HF/HB=HE/HC
Xét ΔFHE và ΔBHC có
HF/HB=HE/HC
\(\widehat{FHE}=\widehat{BHC}\)
Do đó: ΔFHE\(\sim\)ΔBHC
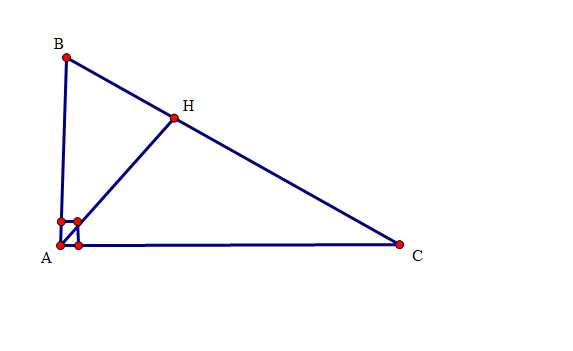

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔHBA\(\sim\)ΔABC
Suy ra: BH/BA=BA/BC
hay \(BA^2=BH\cdot BC\)
b: \(AH=\sqrt{HB\cdot HC}=6\left(cm\right)\)
\(AB=\sqrt{BH\cdot BC}=2\sqrt{13}\left(cm\right)\)
c: Xét ΔAHB vuông tại H có HF là đường cao
nên \(AF\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)
hay AF/AC=AE/AB
Xét ΔAFE vuông tại A và ΔACB vuông tại A có
AF/AC=AE/AB
Do đó:ΔAFE\(\sim\)ΔACB
ôg ơi có hình vẽ k