
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





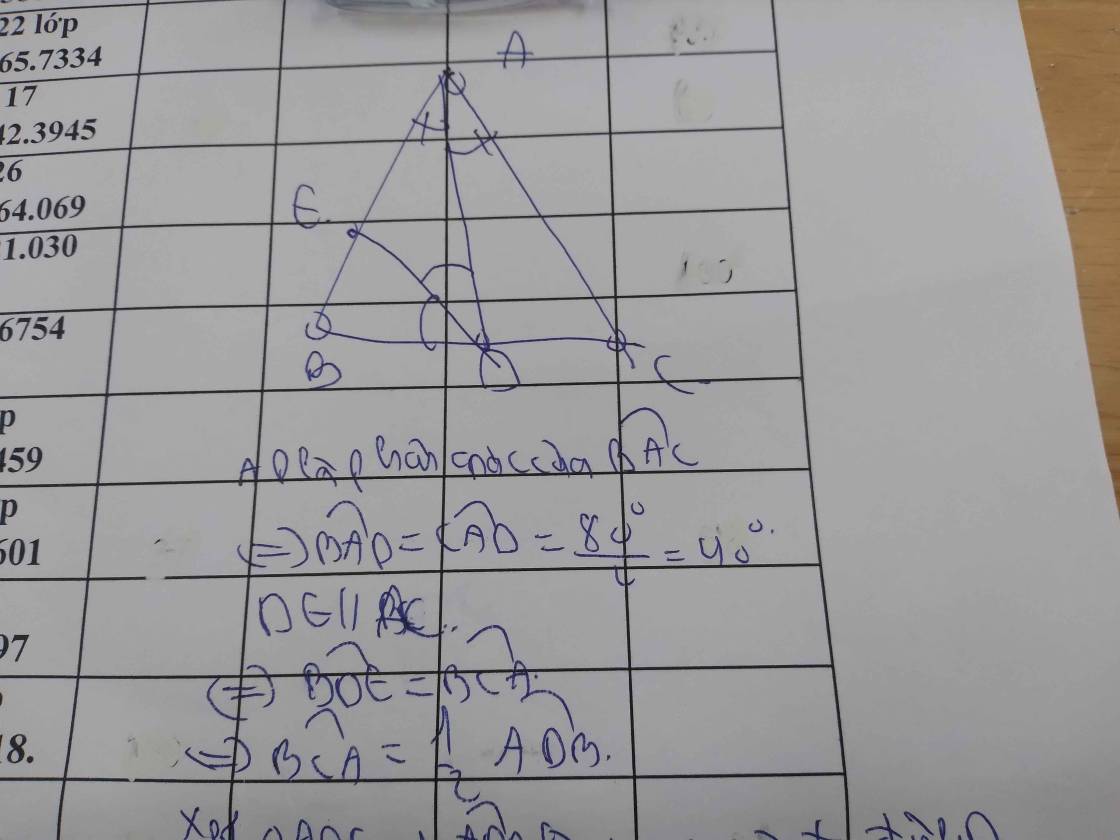
Ta có : góc A + góc B +góc C = 180 ( Định lý tổng 3 góc của 1 tam giác )
80 + 50 + góc C = 180
=> góc C = 180 -80 -50 = 50
Ta có: góc BAC + góc CAx = 180 ( kề bù )
80 + góc Cax = 180
=> Góc Cax = 100
Vì AI là tia phân giác của Góc CAx => góc CAy = góc yAx
=> góc CAy = Góc CAx / 2 =100/2 = 50
Ta có ( góc yAC + góc CAB ) + góc BAC = 180 ( ở vị trí trong cùng phía )
Suy ra Ay // BC ( đpcm)

a, Vì Dx // BC nên: xDC = ACB (hai góc so le trong)
\(\Rightarrow\)ACB=70o.
Xét tam giác ABC có:
ACB+ABC+BAC=180o(tổng ba góc trong một tam giác)
\(\Rightarrow\)ABC=180o-70o-40o=70o.
Vậy ACB=70o; ABC=70o.
b, Ta có:
DAB+BAC=180o (hai góc kề bù).
DAB=180o-40o=140o.
Vì Ay là phân giác của DAB nên DAy = yAB=\(\dfrac{140^o}{2}\)=70o.
\(\Rightarrow\)yAB=ABC=70o. Mà hai góc này ở vị trí so le trong nên Ay // BC.
c,Theo bài, Am là phân giác của BAC nên: BAm = CAm = 20o.
Bn là phân giác của ABC nên: ABn = CBn = 35o.
Mà BEm là góc ngoài tại đỉnh E của tam giác ABE nên:
BEm =35o+20o=55o
Bài giải :
a, Vì Dx // BC nên: xDC = ACB (hai góc so le trong)
⇒ACB=70o.
Xét tam giác ABC có:
ACB+ABC+BAC=180o(tổng ba góc trong một tam giác)
⇒ABC=180o-70o-40o=70o.
Vậy ACB=70o; ABC=70o.
b, Ta có:
DAB+BAC=180o (hai góc kề bù).
DAB=180o-40o=140o.
Vì Ay là phân giác của DAB nên DAy = yAB=140°/2 =70o.
⇒yAB=ABC=70o. Mà hai góc này ở vị trí so le trong nên Ay // BC.
c,Theo bài, Am là phân giác của BAC nên: BAm = CAm = 20o.
Bn là phân giác của ABC nên: ABn = CBn = 35o.
Mà BEm là góc ngoài tại đỉnh E của tam giác ABE nên:
BEm =35o+20o=55o

góc C=180 độ-góc A-góc B
=180-60-80=40 độ
MD//AB
=>góc ADM=góc BAD=60/2=30 độ
DM//AB
=>góc DMC=góc BAC=60 độ

\(a,\widehat{A}+\widehat{B}+\widehat{C}=180\\ \Rightarrow180-3\widehat{C}+\widehat{C}+70=180\\ \Rightarrow-2\widehat{C}=-70\\ \Rightarrow\widehat{C}=35\\ \Rightarrow\widehat{A}=180-35=145\)