Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta thấy ΔAMC và ΔAMB có cùng chiều cao kẻ từ A xuống BC, MC=MB nên
SAMB = SAMC (đpcm)

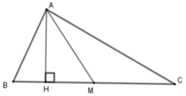
Kẻ AH ⊥ BC tại H. Ta có SABC = 1 2 AH. BC
SAMC = 1 2 AH.MC
Mà AM là đường trung tuyến nên M là trung điểm của BC => BC = 2AM
Từ đó SABC = 1 2 AH. BC = SABC = 1 2 AH. 2MC = 2SAMC
Suy ra SAMC = 1 2 SABC = 1 2 .60 = 30 cm2
Vậy SAMC = 30 cm2
Đáp án cần chọn là: A

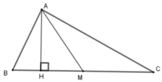
Kẻ AH ⊥ BC tại H. Ta có SABC = 1 2 AH. BC; SAMC = 1 2 AH.MC
Mà AM là đường trung tuyến nên M là trung điểm của BC => BC = 2AM
Từ đó SABC = 1 2 AH. BC = SABC = 1 2 AH. 2MC = 2SAMC
Suy ra SAMC = 1 2 SABC = 1 2 .40 = 20 cm2
Vậy SAMC = 20 cm2
Đáp án cần chọn là: C

a: Sửa đề: BC=10cm và ΔABC vuông tại A
\(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot8=3\cdot8=24\left(cm^2\right)\)
b: Kẻ AH vuông góc BC
\(S_{ABM}=\dfrac{1}{2}\cdot AH\cdot BM\)
\(S_{ACM}=\dfrac{1}{2}\cdot AH\cdot CM\)
mà BM=CM
nên \(S_{ABM}=S_{ACM}\)

A B C M H
Từ A kẻ đường thẳng AH vuông góc với BC ( H thuộc BC )
Ta có : \(S_{ABM}=\frac{1}{2}\cdot BM\cdot AH\)(1)
và \(S_{ACM}=\frac{1}{2}\cdot MC\cdot AH\)(2)
Mặt khác ta có AM là đường trung tuyến
=> \(BM=MC\)(3)
Từ (1), (2) và (3) ta có : \(S_{ABM}=S_{ACM}\left(đpcm\right)\)
kẻ đường cao AH
SABM=1/2BM.AH
SACM=1/2CM.AH
có BM=CM
=>SAMB=SAMC
Ta co : SAMB=\(\frac{1}{2}\)BM.AH
Va : SACM=\(\frac{1}{2}\)CM.AH
Ma : AM là đường trung tuyến của tam giác ABC \(\Rightarrow BM=MC\)
Hay : SAMB=SACM (dpcm)