Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Sử dụng tính chất đường phân giác:
ABAC=BDDC=1520=34(1)ABAC=BDDC=1520=34(1)
Áp dụng định lý Pitago cho tam giác vuông ABCABC:
AB2+AC2=BC2=(BD+DC)2=352=1225(2)AB2+AC2=BC2=(BD+DC)2=352=1225(2)
Từ (1);(2)⇒AB3=AC4⇒AB29=AC216=AB2+AC29+16=122525=49(1);(2)⇒AB3=AC4⇒AB29=AC216=AB2+AC29+16=122525=49
⇒{AB2=49.9AC2=49.16⇒AB=21;AC=28⇒{AB2=49.9AC2=49.16⇒AB=21;AC=28 (cm)

a: Xét ΔCBA có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{BD}{30}=\dfrac{CD}{40}\)
=>\(\dfrac{BD}{3}=\dfrac{CD}{4}\)
mà BD+CD=50
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{50}{7}\)
=>\(BD=\dfrac{150}{7}\left(cm\right);CD=\dfrac{200}{7}\left(cm\right)\)
Xét ΔABC có DE//AB
nên \(\dfrac{DE}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{DE}{30}=\dfrac{200}{7}:50=\dfrac{4}{7}\)
=>\(DE=\dfrac{120}{7}\left(cm\right)\)
b: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
=>Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot30\cdot40=15\cdot40=600\left(cm^2\right)\)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=10^2-6^2=64\)
hay AC=8(cm)
Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)(Tính chất đường phân giác của tam giác)
hay \(\dfrac{AD}{6}=\dfrac{CD}{10}\)
mà AD+CD=AC(D nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{AC}{16}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{AD}{6}=\dfrac{1}{2}\\\dfrac{CD}{10}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AD=3\left(cm\right)\\CD=5\left(cm\right)\end{matrix}\right.\)
Vậy: AC=8cm; AD=3cm; CD=5cm
b) Xét ΔDHC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔDHC\(\sim\)ΔABC(g-g)


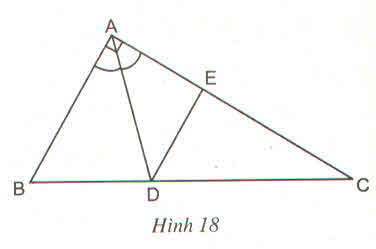

Cần giải giúp gấp ngày mai mình cần rồi ạ