Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kí hiệu S là diện tích.
Từ E kẻ song song với BC, cắt AC tại N.
Nối B với N.
Vì ENCB là hình thang nên S\(_{ECB}\) = S\(_{NCB}\) ( chung đáy, chiều cao đều bằng chiều cao hình thang ENCB )
Vì AE = \(\frac{3}{4}\) AB suy ra BE = \(\frac{1}{4}\) AB
Ta có :
S\(_{EBC}\) = \(\frac{1}{4}\) S\(_{ABC}\) ( BE = \(\frac{1}{4}\) AB, chung chiều cao hạ từ C xuống AB )
S\(_{EBC}\) là :
48 x \(\frac{1}{4}\) = 12 ( cm\(^2\) )
Đáp số : 12 cm\(^2\) .

Lời giải:
Ta có:
$\frac{S_{CEA}}{S_{CAB}}=\frac{AE}{AB}=\frac{1}{4}$
$S_{CEA}=S_{CAB}\times \frac{1}{4}=48\times \frac{1}{4}=12$ (cm2)
$S_{CEB}=S_{ABC}-S_{CEA}=48-12=36$ (cm2)

mình cũng muốn có câu trả lời. các bạn giúp mình và Quỳnh Trang nhé
A B C H E
Theo bài ta có : \(AE=\frac{3}{4}AB\Rightarrow BE=\frac{1}{4}AB\)
Gọi CH là đường cao của tam giác ABC
\(\Rightarrow S_{ABC}=\frac{1}{2}\cdot CH\cdot AB=48\left(m^2\right)\)
Xét tam giác BEC có CH là đường cao tương ứng với đáy EB
\(\Rightarrow S_{BEC}=\frac{1}{2}\cdot BE\cdot CE\)
\(=\frac{1}{2}\cdot\frac{1}{4}\cdot AB\cdot CH=\frac{1}{8}\cdot48=6\left(m^2\right)\)

Ta nối E với B để được tam giác AEB
Diện tích của tam giác AEB là:
34,8 : 2 x 3 = 52,2 cm²
Diện tích của tam giác ABC là:
52,2 : 3 x 4 = 69,6 cm²
k nhé

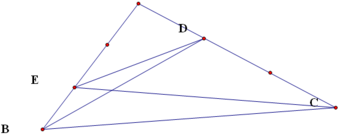
A B C E D
Mình biểu diễn bằng hình vẽ trên.
Xét EAD và EDB chung đỉnh E, đáy AD gấp 2 lần đáy DB (10 : (15 -10) = 2)
=> S_EAD gấp 2 lần S_EDB => Diện tích EDB = 45 : 2 = 22,5 (cm2)
Diện tích BAE là : 45 + 22,5 = 67,5 (cm2)
Xét tam giác BAE và tam giác AEC có chung đỉnh B và đáy AE gấp 3 lần đáy EC (15 : (20-15) = 3)
=> Diện tích BAE gấp 3 lần diện tích AEC. Vậy diện tích AEC là : 67,5 : 3 =22,5 (cm2)
Vậy diện tích ABC là : 67,5 + 22,5 = 90 (cm2)