Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu hỏi này sai!!! Vì BA=BC mà BE=BA. =>BC=BE. mà E nằm trên BC =>BE trùng với BC.
Câu a: có thể tính
Câu b: 2 điểm A và F trung nhau, 2 điểm C và E trùng nhau nên không phải đoạn thẳng
Câu c: theo câu b=> không thể song song

BCEDAF
*Hình quên đánh dấu ABD = DBE nhé
*Cần viết gt và kl thì bảo mình nhá <3
Giải
a) Xét ∆ABD và ∆EBD có :
AB = BE (gt) |
FBD = DBE (AD là tia phân giác ABE) }
BD là cạnh chung |
=> ∆ABD = ∆EBD (c.g.c)

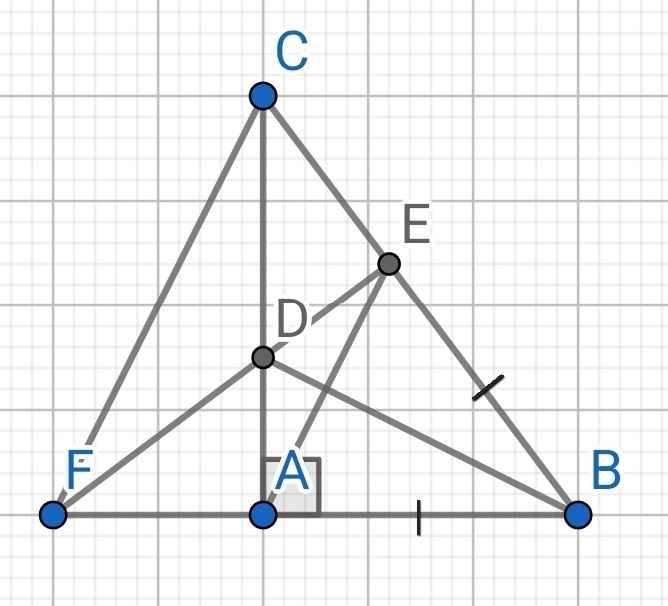 a) Xét ∆ABD và ∆EBD có:
a) Xét ∆ABD và ∆EBD có:
AB = BE (gt)
∠ABD = ∠EBD (BD là tia phân giác của ABC)
BD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ AD = ED (hai cạnh tương ứng)
Lại do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED = 90⁰ (hai góc tương ứng)
⇒ ∠DAF = ∠DEC = 90⁰
Xét hai tam giác vuông: ∆DAF và ∆DEC có:
AD = ED (cmt)
∠ADF = ∠EDC (đối đỉnh)
⇒ ∆DAF = ∆DEC (cạnh góc vuông - góc nhọn kề)
⇒ AF = EC (hai cạnh tương ứng)
c) ∆BAE có:
AB = BE (gt)
⇒ ∆BAE cân tại B
⇒ ∠BEA = ∠BAE = (180⁰ - ∠ABC) : 2 (1)
Do AF = EC (cmt)
AB = BE (gt)
⇒ AF + AB = EC + BE
⇒ BF = BC
⇒ ∆BFC cân tại B
⇒ ∠BCF = ∠BFC = (180⁰ - ∠ABC) : 2 (2)
Từ (1) và (2) suy ra:
∠BEA = ∠BCF
Mà ∠BEA và ∠BCF là hai góc đồng vị
⇒ AE // CF

B tham khảo lời giải trong này xemm https://cunghocvui.com/danh-muc/toan-lop-7

a,Xét tam giác ABM và tam giác EBM có :
AB = BE (gt)
góc B1 =góc B2(gt)
BM:cạnh chung
Suy ra tam giác ABM = tam giác EBM(c-g-c)
b,Do tam giác ABM = tam giác EBM ( cm câu a)
Suy ra AM = EM ( cặp cạnh tương ứng )
c,Do tam giác ABM = tam giác EBM ( cm câu a)
Suy ra góc BAM = góc BEM ( cặp cạnh tương ứng )
Mà góc BAM = 90 độ
Suy ra góc BEM = 90 độ
Bài làm đúng 100% đó,chúc bạn học tốt nhé!^.<

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng
a. xét tam giác (tg) ABM và tg EBM ta có:
AB = BE (gt); góc ABM = góc MBE (BM là phân giác của góc B), AM chung
=> tg ABM = tg EBM (c-g-c)
b. ta có: tg ABM = tg EBM => góc BAM = góc BEM => góc FAM = góc CEM
lại có: AM = ME (tg ABM = tg EBM)
mà góc AMF = góc EMC (đối đỉnh)
từ 3 điều trên => tg AMF = tg EMC (g-c-g)
=> AF = EC
c. ta có: AB = BE (gt) => tg ABE cân tại B, có BM là đường phân giác đồng thời là đường cao
=> BM vuông góc AE (1)
lại có BF = BC (AB = BE; AF = EC) => tg BFC cân tại B, có BM là đường phân giác đồng thời là đường cao
=> BM vuông góc CF (2)
(1), (2) => AE // CF
Hình bạn ưi