Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn dùng định lý Ta - lét đảo trong tam giác là tính được.
Chúc bạn học tốt

Ta có: \(AD=DE=EF=FB=\dfrac{1}{4}AB\) và \(AM=MN=NP=PC=\dfrac{1}{4}AC\)
Xét \(\Delta ABC\) có: \(\dfrac{AE}{AB}=\dfrac{AN}{AC}=\dfrac{1}{2}\)
\(\Rightarrow EN//BC\) \(\Rightarrow\) EN là đường trung bình của tam giác ABC
\(\Rightarrow EN=\dfrac{BC}{2}=\dfrac{15}{2}=7,5\left(cm\right)\)
Tương tự với tam giác AEN có: \(\dfrac{AD}{AE}=\dfrac{AM}{AN}=\dfrac{1}{2}\)\(\Rightarrow DM//EN\)
\(\Rightarrow\)DM là đường trung bình của tam giác AEN
\(\Rightarrow DM=\dfrac{EN}{2}=\dfrac{7,5}{2}=3,75\left(cm\right)\)
Lại có: \(\dfrac{AE}{AF}=\dfrac{AN}{AP}=\dfrac{2}{3}\)
Áp dụng định lí Ta-let đảo ta có: \(\dfrac{AE}{AF}=\dfrac{AN}{AP}=\dfrac{EN}{FP}=\dfrac{2}{3}\Leftrightarrow\dfrac{7,5}{FP}=\dfrac{2}{3}\Rightarrow FP=11,25cm\)

a) Ta có:
\(\frac{{AE}}{{AC}} = \frac{{10}}{{15}} = \frac{2}{3};\frac{{AF}}{{AB}} = \frac{8}{{12}} = \frac{2}{3}\)
Xét tam giác \(AFE\) và tam giác \(ABC\) ta có:
\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}} = \frac{2}{3}\)
\(\widehat A\) chung
Do đó, \(\Delta AFE\backsim\Delta ABC\) (c.g.c)
Do đó, \(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}} = \frac{{EF}}{{BC}} = \frac{2}{3}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Do đó, \(\frac{{EF}}{{BC}} = \frac{2}{3} \Rightarrow EF = \frac{{BC.2}}{3} = \frac{{18.2}}{3} = 12\)
Vậy \(BC = 12cm\).
b) Vì \(FC = FD\) nên tam giác \(FDC\) cân tại \(F\).
Suy ra, \(\widehat {FDC} = \widehat {FCD}\) (tính chất)
Ta có:
\(\frac{{AC}}{{MD}} = \frac{{15}}{{20}} = \frac{3}{4};\frac{{BC}}{{DE}} = \frac{9}{{12}} = \frac{3}{4}\)
Xét tam giác \(ABC\) và tam giác \(MED\) ta có:
\(\frac{{AC}}{{MD}} = \frac{{BC}}{{DE}} = \frac{3}{4}\)
\(\widehat {FCD} = \widehat {FDC}\) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta MED\) (c.g.c).

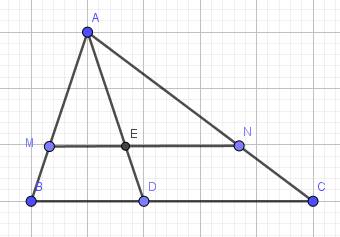
\(\Delta ABC\) có:
\(\dfrac{AM}{AB}=\dfrac{8}{12}=\dfrac{2}{3}\)
\(\dfrac{AN}{AC}=\dfrac{12}{15}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{2}{3}\)
\(\Rightarrow\) MN // BC (định lý Ta-lét)
\(\Delta AME\) và \(\Delta ABD\) có:
ME // BD (do MN // BC)
\(\Rightarrow\dfrac{AE}{AD}=\dfrac{AM}{AB}=\dfrac{2}{3}\) (hệ quả của định lý Ta-lét)

