Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

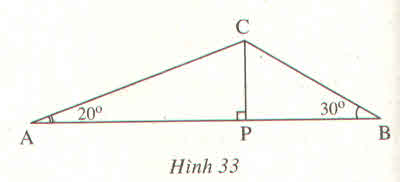
Đặt AP=x suy ra BP=60-x.Ta có phương trình
xtg\(20^0\)=(60-x)tg\(30^0\)
Đ/s:AP ≈36,801cm;BP=23,119cm;CP=13,396cm
Tham khảo nha

Gọi O là tâm đường tròn \(\Rightarrow\) O là trung điểm BC
\(\stackrel\frown{BE}=\stackrel\frown{ED}=\stackrel\frown{DC}\Rightarrow\widehat{BOE}=\widehat{EOD}=\widehat{DOC}=\dfrac{180^0}{3}=60^0\)
Mà \(OD=OE=R\Rightarrow\Delta ODE\) đều
\(\Rightarrow ED=R\)
\(BN=NM=MC=\dfrac{2R}{3}\Rightarrow\dfrac{NM}{ED}=\dfrac{2}{3}\)
\(\stackrel\frown{BE}=\stackrel\frown{DC}\Rightarrow ED||BC\)
Áp dụng định lý talet:
\(\dfrac{AN}{AE}=\dfrac{MN}{ED}=\dfrac{2}{3}\Rightarrow\dfrac{EN}{AN}=\dfrac{1}{2}\)
\(\dfrac{ON}{BN}=\dfrac{OB-BN}{BN}=\dfrac{R-\dfrac{2R}{3}}{\dfrac{2R}{3}}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{EN}{AN}=\dfrac{ON}{BN}=\dfrac{1}{2}\) và \(\widehat{ENO}=\widehat{ANB}\) (đối đỉnh)
\(\Rightarrow\Delta ENO\sim ANB\left(c.g.c\right)\)
\(\Rightarrow\widehat{NBA}=\widehat{NOE}=60^0\)
Hoàn toàn tương tự, ta có \(\Delta MDO\sim\Delta MAC\Rightarrow\widehat{MCA}=\widehat{MOD}=60^0\)
\(\Rightarrow\Delta ABC\) đều

1: góc BFC=góc BEC=90 độ
=>BFEC nộitiếp
Tâm là trung điểm của BC
2: góc EFC=góc DAC
góc DFC=góc EBC
góc DAC=góc EBC
=>góc EFC=góc DFC
=>FC là phân giác của góc EFD
BFEC nội tiếp
=>góc AFE=góc ACB
mà góc A chung
nên ΔAFE đồng dạng với ΔACB
=>AF/AC=AE/AB
=>AF*AB=AC*AE

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: góc DFC=góc EBC
góc EFC=góc DAC
góc EBC=góc DAC
=>góc DFC=góc EFC
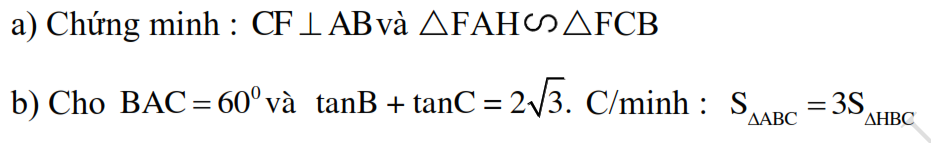


a: Xét ΔBAC có
AD là đường cao ứng với cạnh BC
BE là đường cao ứng với cạnh AC
AD cắt BE tại H
Do đó: H là trực tâm của ΔBAC
Suy ra: CH\(\perp\)AB tại F
Xét ΔFAH vuông tại F và ΔFCB vuông tại F có
\(\widehat{FAH}=\widehat{FCB}\left(=90^0-\widehat{FBC}\right)\)
Do đó: ΔFAH\(\sim\)ΔFCB