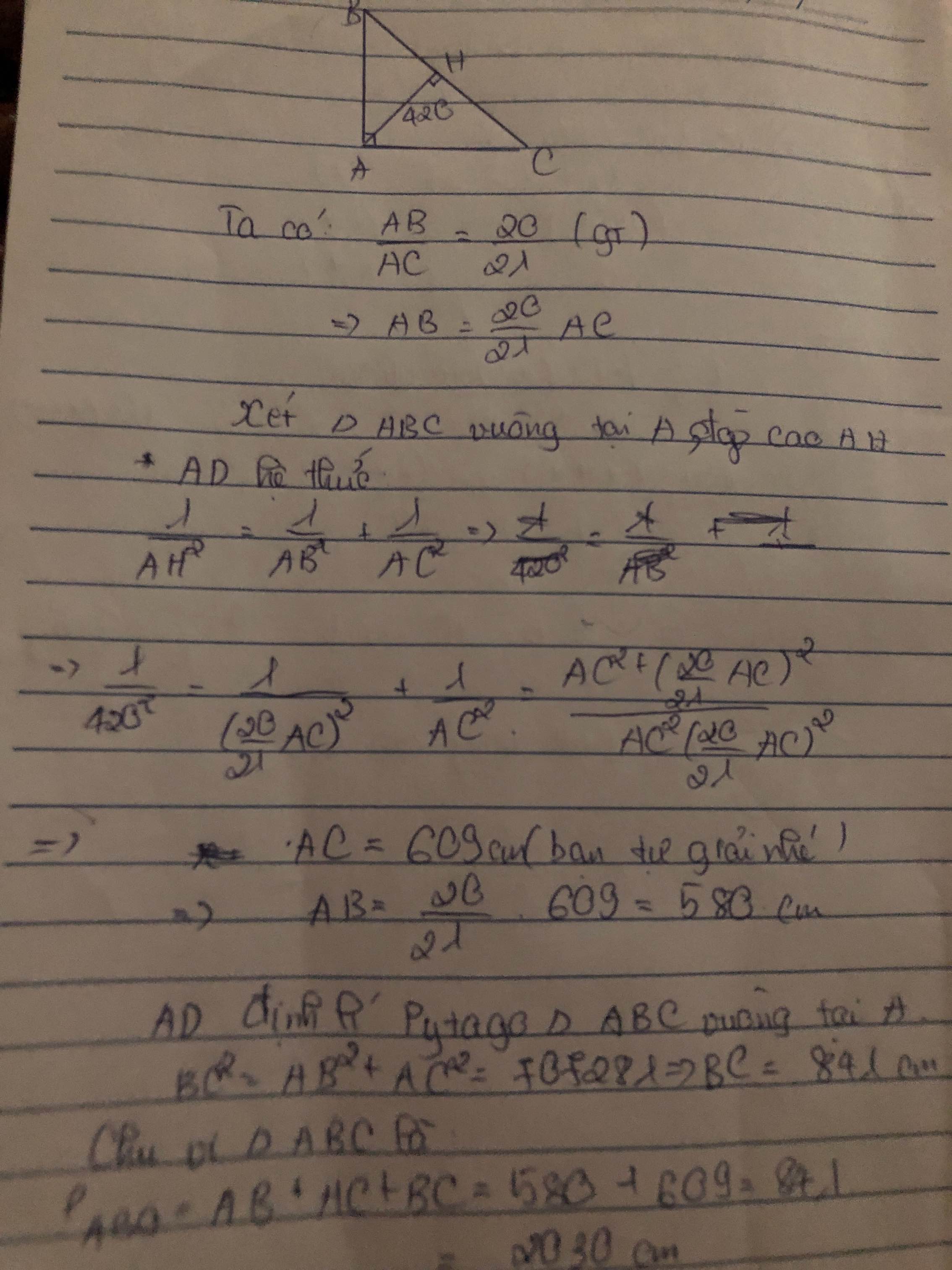Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: AB/AC=5/7
=>HB/HC=(AB/AC)^2=25/49
=>HB/25=HC/49=k
=>HB=25k; HC=49k
ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
=>1225k^2=15^2=225
=>k^2=9/49
=>k=3/7
=>HB=75/7cm; HC=21(cm)

Tam giac ABC đồng dạng tam giác HAC (cùng vuông và có chung góc C)
AB/AC = AH/HC = 20/21
HC = 21AH/20 = 441
==> AC = căn(AH^2 + HC^2) =căn(420^2 + 441^2) = 609
AB/AC = 20/21
AB = 20/21*609 = 580
BC = căn(AB^2 + AC^2) = căn(580^2 + 609^2) = 841
Chu vi tam giác ABC = tổng 3 cạnh
C = AB + AC + BC = 580 + 609 + 841 = 2030

A B C H
Tam giác ABC vuông tại A, áp dụng hệ thức, ta có:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{18^2}=\frac{1}{324}\) (1)
Đặt \(\frac{AB}{AC}=\frac{3}{4}\Rightarrow\frac{AB}{3}=\frac{AC}{4}=k\Rightarrow AB=3k;AC=4k\)
Thế vào (1) ta được: \(\frac{1}{\left(3k\right)^2}+\frac{1}{\left(4k\right)^2}=\frac{1}{324}\)
\(\Rightarrow\frac{9k^2+16k^2}{9k^2.16k^2}=\frac{1}{324}\)
\(\Rightarrow\frac{15k^2}{144k^4}=\frac{1}{324}\Rightarrow\frac{15}{144k^2}=\frac{1}{324}\Rightarrow144k^2=4860\Rightarrow k^2=33,75\Rightarrow k=\frac{3\sqrt{15}}{2}\)
\(\Rightarrow AB=\frac{3\sqrt{15}}{2}.3=\frac{9\sqrt{15}}{2}\) (cm)
AC = (3 √15)/2 . 4 = 6 √15 (cm)
Tam giác ABC vuông tại A, áp dụng định lý Pitago ta có:
AB2 + AC2 = [(9 √15)/2]^2+(6 √15)^2= 3375/4 = BC2
=> BC = (15 √15)/2
Vậy chu vi của tam giác ABC là: AB+BC+AC= (9 √15)/2 + 6 √15 + (15 √15)/2 = 18 √15 (cm)

\(\dfrac{AB}{AC}=\dfrac{20}{21}\Rightarrow AB=\dfrac{20AC}{21}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{420^2}=\dfrac{1}{\left(\dfrac{20}{21}AC\right)^2}+\dfrac{1}{AC^2}=\dfrac{841}{400AC^2}\)
\(\Rightarrow AC=609\) \(\Rightarrow AB=\dfrac{20}{21}AC=580\)
\(BC=\sqrt{AB^2+AC^2}=841\)
Chu vị: \(609+580+841=2030\)

Xét tam giác ABC vuông tại A:
\(BC^2=AB^2+AC^2\left(Pytago\right)\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{20^2+15^2}=25\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A:
\(AH.BC=AB.AC\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{20.15}{25}=12\left(cm\right)\)
Ta có: \(P_{ABC}=AB+AC+BC=20+15+25=60\left(cm\right)\)

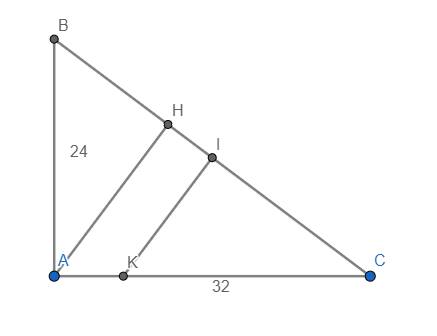
Ta có \(\widehat{HAC}=\widehat{B}\) (cùng phụ với \(\widehat{C}\))
Mà \(\widehat{B}=\tan^{-1}\left(\dfrac{AC}{AB}\right)=\tan^{-1}\left(\dfrac{32}{24}\right)=\tan^{-1}\left(\dfrac{4}{3}\right)\approx53,13^o\)
Nên \(\widehat{HAC}\approx53,13^o\)
Ta có \(BC=\sqrt{AB^2+AC^2}=\sqrt{24^2+32^2}=40\) cm
\(\Rightarrow IB=IC=20cm\)
Ta có \(CH=\dfrac{AC^2}{BC}=\dfrac{32^2}{40}=25,6cm\)
\(AH=\dfrac{AB.AC}{BC}=\dfrac{24.32}{40}=19,2cm\)
Do vậy \(\dfrac{CI}{CH}=\dfrac{IK}{AH}\Rightarrow IK=\dfrac{CI.AH}{CH}=\dfrac{20.19,2}{25,6}=15cm\)
Mặt khác \(\dfrac{CI}{CH}=\dfrac{CK}{CA}\Rightarrow CK=\dfrac{CI.CA}{CH}=\dfrac{20.32}{25,6}=25cm\)
\(\Rightarrow C_{CIK}=CI+CK+IK\) \(=20+15+25=60cm\)
Mặt khác, \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.24.32=384cm^2\)
Lại có \(\Delta CIK~\Delta CAB\left(g.g\right)\) \(\Rightarrow\dfrac{S_{CIK}}{S_{CAB}}=\left(\dfrac{IK}{AB}\right)^2=\left(\dfrac{15}{24}\right)^2=\dfrac{25}{64}\)
\(\Rightarrow S_{CIK}=\dfrac{25}{64}S_{CAB}=\dfrac{25}{64}.384=150cm^2\)

`(AB)/(AC)=2/3 = (2x)/(3x) (x >0)`
Áp dụng hệ thức lượng trong tam giác vuông:
`1/(AH^2)=1/(AB^2)+1/(AC^2)`
`<=>1/(6^2)=1/(4x^2)+1/(9x^2)`
`<=> x=\sqrt13`
`=> AB=2\sqrt13 (cm) ; AC=3\sqrt13 (cm)`
Áp dụng định lí Pytago:
`AB^2+AC^2=BC^2`
`=> BC=13(cm)`
`=>` Chu vi là: `13+5\sqrt13 (cm)`.