Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

-Qua E,F kẻ các đường thẳng song song với BC cắt AM lần lượt tại P,Q.
-Xét △PIF có: PF//EQ (gt).
\(\Rightarrow\dfrac{EQ}{PF}=\dfrac{IE}{IF}\) (hệ quả định lí Ta-let).
-Xét △ABM có: EQ//BM (gt).
\(\Rightarrow\dfrac{EQ}{BM}=\dfrac{AE}{AB}\) (hệ quả định lí Ta-let). (1)
-Xét △ACM có: PF//CM (gt).
\(\Rightarrow\dfrac{PF}{CM}=\dfrac{AF}{AC}\) (hệ quả định lí Ta-let).
Mà \(BM=CM\) (M là trung điểm BC), \(AE=AF\) (gt)
\(\Rightarrow\dfrac{PF}{BM}=\dfrac{AE}{AC}\) (2)
-Từ (1), (2) suy ra:
\(\dfrac{\dfrac{EQ}{BM}}{\dfrac{PF}{BM}}\)=\(\dfrac{\dfrac{AE}{AB}}{\dfrac{AE}{AC}}\)
\(\Rightarrow\) \(\dfrac{EQ}{PF}=\dfrac{AC}{AB}\) mà \(\dfrac{EQ}{PF}=\dfrac{IE}{IF}\left(cmt\right)\)
Nên \(\dfrac{IE}{IF}=\dfrac{AC}{AB}\)

a: Gọi K là trung điểm của BD
Suy ra: AD=DK=BK
Xét ΔBDC có
M là trung điểm của BC
K là trung điểm của BD
Do đó: MK là đường trung bình của ΔBDC
Suy ra: MK//CD
hay MK//ID
Xét ΔAMK có
D là trung điểm của AK
DI//KM
Do đó: I là trung điểm của AM
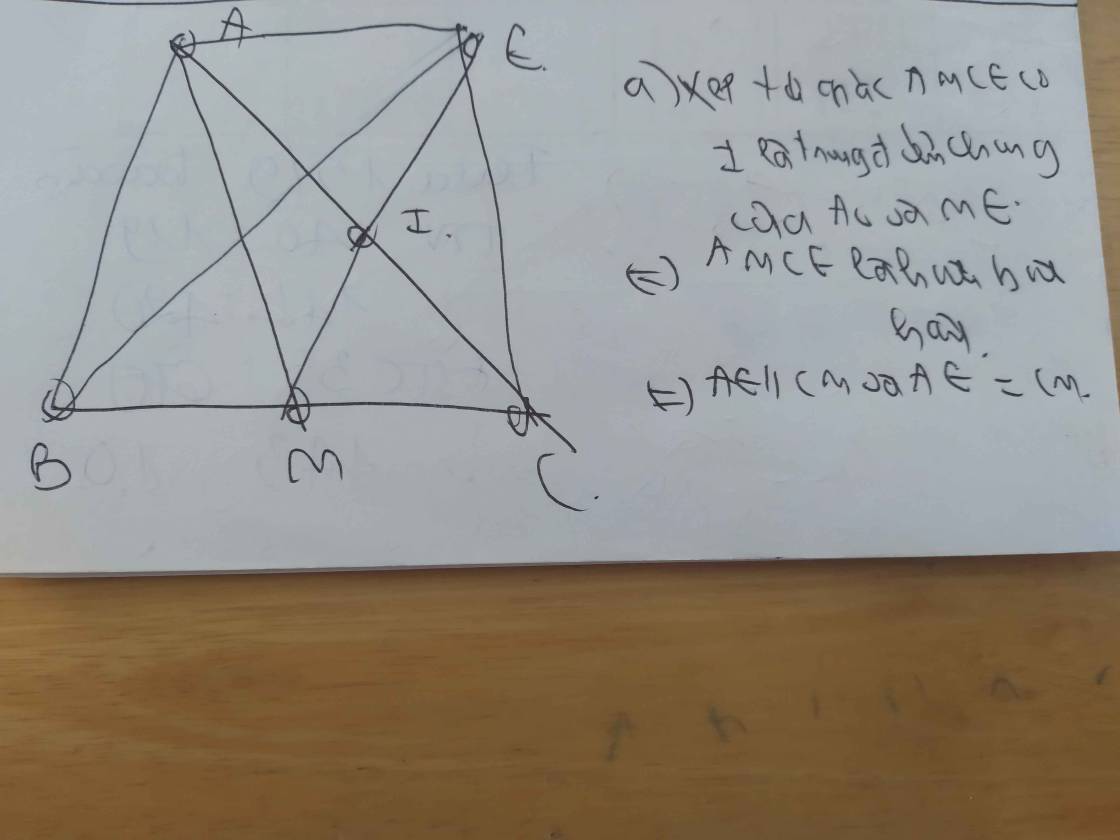

mình cũng đang cần bài này nè ta lét phải ko?