Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

D K C B E 1 2
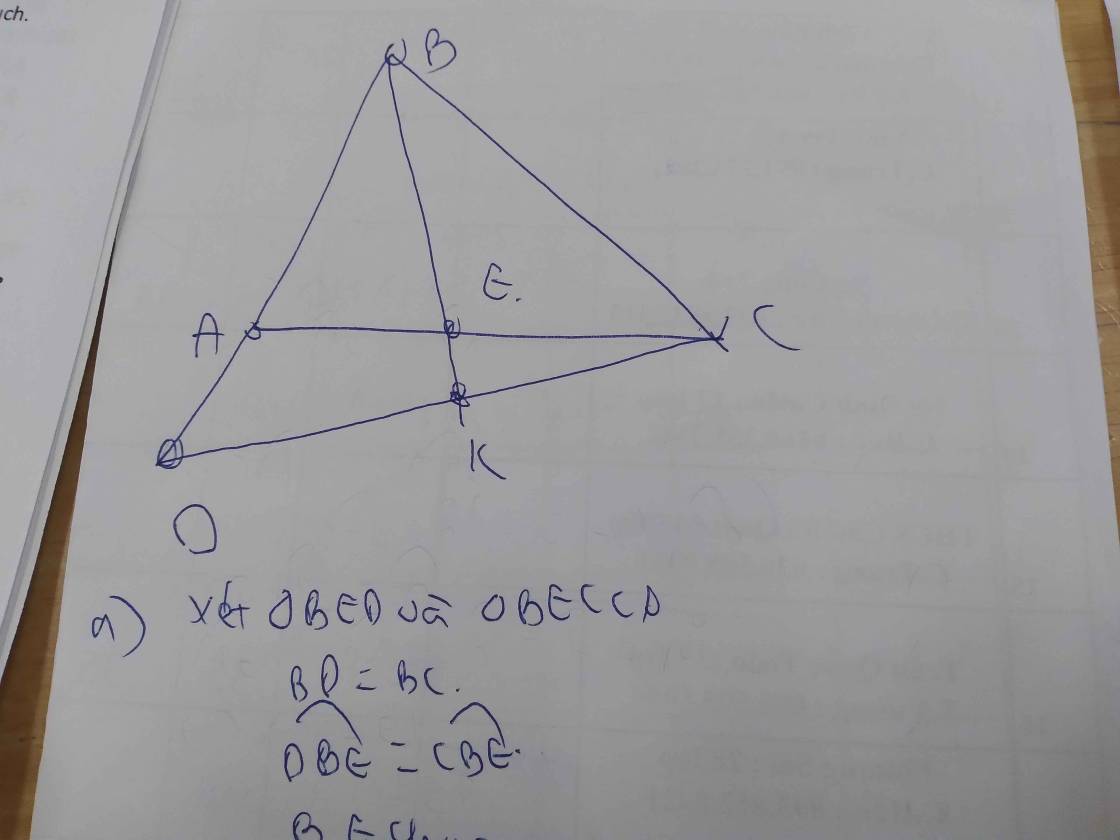
a)Xét tam giác BED và tam giác BEC có:
BD=BC(gt)
Góc B1= góc B2 (Vì BK là tia phân giác của góc B)
BE chung
=> Tam giác BED= tam giác BEC(c.g.c)
b) Xét tam giác BKS và tam giác BKC có:
BK chung
Góc B1= góc B2 (Vì BK là tia phân giác của góc B)
DK=KC( vì K là trung điểm của DC)
=> Tam giác BKD= tam giác BKC(c.g.c)
=>BK vg góc với DC
hay EK vg góc với DC
c)VÌ EK vg góc với DC(cm b)
Mà BK vg góc với DC(cm b)
=> EK và BK cùng vg góc với DC
=> Ek trùng với BK
=>Ba điểm B,E,K thẳng hàng

a: Xét ΔBDE và ΔBCE có
BD=BC
\(\widehat{DBE}=\widehat{CBE}\)
BE chung
Do đó: ΔBDE=ΔBCE
b: Ta có: ΔBDE=ΔBCE
=>ED=EC
=>E nằm trên đường trung trực của DC(1)
Ta có: BD=BC
=>B nằm trên đường trung trực của CD(2)
Ta có: KD=KC
=>K nằm trên đường trung trực của CD(3)
Từ (1),(2),(3) suy ra B,E,K thẳng hàng
=>B,E,K cùng nằm trên đường trung trực của DC
=>EK\(\perp\)DC
c: ΔAHD vuông tại H có \(\widehat{DAH}=45^0\)
nên ΔAHD vuông cân tại H
Xét ΔBDC có BD=BC
nên ΔBCD cân tại B
mà \(\widehat{BDC}=45^0\)
nên ΔBCD vuông cân tại B
=>\(\widehat{ABC}=90^0\)

B C A D I E 1 2 H
a, Xét tam giác BED và tam giác BEC có:
BE chung
góc B1= góc B2
BC=BD
=> tam giác BED = tam giác BEC (c.g.c)
Xét tam giác BDI và tam giác BCI có:
BI chung
góc B1= góc B2
BD=BC
=> tam giác BDI = tam giác BCI (c.g.c)
=> DI=CI
b,Vì BD=BC => tam giác BDC cân tại B
Mà BI là tia phân giác góc B
=> BI đồng thời là đường cao
=> BI vuông góc với DC
Mà AH vuông góc với DC
=> BI//AH
A B C D E I H
Cm: a) Xét t/giác BED và t/giác BEC
có: BD = BC (gt)
\(\widehat{DBE}=\widehat{CBE}\)(gt)
BE : chung
=> t/giác BED = t/giác BEC (c.g.c)
Ta có: BD = BC (gt) => t.giác BCD cân
Mà BI là tia p/giác góc B của t/giác BCD
=> BI đồng thời là đường trung tuyến (t/c t/giác cân)
=> IC = ID
(phần này có thể xét 2 t/giác BID và t/giác BIC)
b) Ta có: t/giác BCD cân tại B
BI là tia p/giác của t/giác BCD
=> BI đồng thời là đường cao của t/giác (t/c của t/giác cân)
=> BI \(\perp\)DC
mà AH \(\perp\)DC
=> AH // BI (từ \(\perp\) đến //)

a) Xét ΔBED và ΔBEC có
BD=BC(gt)
\(\widehat{DBE}=\widehat{CBE}\)(BE là tia phân giác của \(\widehat{DBC}\))
BE chung
Do đó: ΔBED=ΔBEC(c-g-c)
Xét ΔBDI và ΔBCI có
BD=BC(gt)
\(\widehat{DBI}=\widehat{CBI}\)(BI là tia phân giác của \(\widehat{DBC}\))
BI chung
Do đó: ΔBDI=ΔBCI(c-g-c)
⇒ID=IC(hai cạnh tương ứng)
b) Sửa đề: Chứng minh AH//BI
Xét ΔBDC có BD=BC(gt)
nên ΔBDC cân tại B(Định nghĩa tam giác cân)
Ta có: ΔBDC cân tại B(cmt)
mà BI là đường phân giác ứng với cạnh đáy DC(gt)
nên BI là đường cao ứng với cạnh DC(Định lí tam giác cân)
⇒BI⊥DC
Ta có: AH⊥DC(gt)
BI⊥DC(cmt)
Do đó: AH//BI(Định lí 1 từ vuông góc tới song song)