Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
góc HAM=góc KAM
=>ΔAHM=ΔAKM
=>AH=AK
Xét ΔACB co AH/AB=AK/AC
nên HK//BC

a, xét △ AMB và △ AMC có:
AB=AC(gt)
góc BAM=góc CAM (gt)
AM chung
=> △ AMB= △ AMC(c.g.c)
b,xét △ AHM và △ AKM có:
AM cạnh chung
góc HAM=ˆgóc KAM (gt)
=>△ AHM= △ AKM(CH-GN)
=> AH=AK
c,gọi I là giao điểm của AM và HK
xét △ AIH và △ AIK có:
AH=AK(theo câu b)
góc AIH=ˆgóc AIK (gt)
AI chung
=> △ AIH=△ AIK (c.g.c)
=> góc AIH=ˆgóc AIK
mà góc AIH+góc AIK=180độ(2 góc kề bù)
=> HK ⊥ AM

Nếu tam giác ABC mà vuông tại A thì 2 tam giác ABM và ACM không thể bằng nhau đc
Mk nghĩ bn nên xem lại đề bài.

\(MH\perp AB\left(gt\right)\Rightarrow\widehat{MHA}=\widehat{MHB}=90^0\)
\(MK\perp AC\left(gt\right)\Rightarrow\widehat{MKA}=\widehat{MKC}=90^0\)
M là trung điểm của BC (gt) nên MB = MC
AM là tia phân giác của góc A (gt) \(\Rightarrow\widehat{BAM}=\widehat{CAM}\Rightarrow\widehat{HAM}=\widehat{KAM}\)
\(\Delta AHM=\Delta AKM\left(ch-gn\right)\Rightarrow HM=KM\) (2 cạnh tương ứng)
\(\Delta HMB=\Delta KMC\left(ch-cgv\right)\Rightarrow\widehat{B}=\widehat{C}\) ( 2 góc t/ứ)

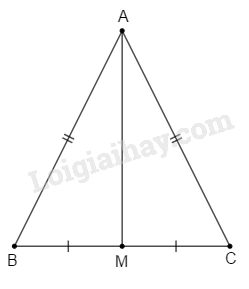
Xét \(\Delta ABC\) có:
c) Ta có \(\Delta ABC\) cân tại \(A\left(cmt\right).\)
=> \(\widehat{B}=\widehat{C}\) (tính chất tam giác cân).
Xét 2 \(\Delta\) vuông \(HBM\) và \(KCM\) có:
\(\widehat{MHB}=\widehat{MKC}=90^0\left(gt\right)\)
\(BM=CM\) (như ở trên)
\(\widehat{B}=\widehat{C}\left(cmt\right)\)
=> \(\Delta HBM=\Delta KCM\) (cạnh huyền - góc nhọn).
=> \(HM=KM\) (2 cạnh tương ứng).
Chúc bạn học tốt!



giúp mình câu d thôi ạ
sai đề hay sao ý bn