Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ΔABC đồng dạng với ΔA'B'C'
=>\(\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}=\dfrac{A'C'}{AC}\)
A'B'=10,8+16,2=27(cm)
=>\(\dfrac{B'C'}{24.3}=\dfrac{A'C'}{32.7}=\dfrac{16.2}{27}=\dfrac{3}{5}\)
=>B'C'=14,58cm; A'C'=19,62(cm)

Vì
△
A'B'C' đồng dạng
△
ABC nên 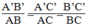
Mà AB = 16,2 cm; BC = 24,3 cm; AC = 32,7 cm nên:
A'B'= AB - 5,4 = 16,2 - 5,4 =10,8 (cm)
Ta có: 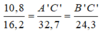
Suy ra: A'C' = (10,8 . 32,7): 16,2 = 21,8 (cm)
B'C'= (10,8 . 24,3): 16,2 = 16,2 (cm)

Vì
△
A'B'C' đồng dạng
△
ABC nên 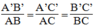
Mà AB = 16,2 cm; BC = 24,3 cm; AC = 32,7 cm nên:
A'B'= AB + 10,8cm = 16,2 + 10,8 = 27 (cm)
Ta có: 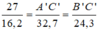
Suy ra: 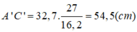
Suy ra: 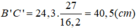

Ta có
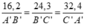
a) Tính được A'B' = 6,2cm. Từ đó tính được B'C' = 9,3cm và A'C' = 12,4cm.
b) Tương tự câu a tính được A'B' = 26,2cm, B'C' = 39,3cm và A'C' = 52,4cm

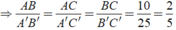
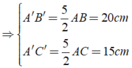
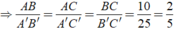
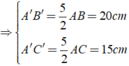
A B C 16,2 24,3 32,7
a) Xét \(\Delta A'B'C',\Delta ABC\) có:
\(\dfrac{A'B'}{AB}=\dfrac{A'C'}{AC}=\dfrac{B'C'}{BC}\left(\Delta A'B'C'\sim\Delta ABC\right)\)
Hay : \(\dfrac{16,2+10,8}{16,2}=\dfrac{A'C'}{32,7}=\dfrac{B'C'}{24,3}\)
=> \(\dfrac{A'C'}{32,7}=\dfrac{B'C'}{24,3}=\dfrac{27}{16,2}\)
=> \(\left\{{}\begin{matrix}A'C'=\dfrac{27.32,7}{16,2}=54,5\left(cm\right)\\B'C'=\dfrac{27.24,3}{16,2}=40,5\left(cm\right)\end{matrix}\right.\)
Vậy các cạnh của \(\Delta A'B'C'\) có độ dài là:
\(A'B'=27cm\)
\(A'C'=54,5cm\)
\(B'C'=40,5cm\)
b) Ta có : \(\dfrac{A'B'}{AB}=\dfrac{A'C'}{AC}=\dfrac{B'C'}{BC}\left(\Delta A'B'C'\sim\Delta ABC-gt\right)\)
Hay : \(\dfrac{16,2-5,4}{16,2}=\dfrac{A'C'}{32,7}=\dfrac{B'C'}{24,3}\)
=> \(\dfrac{A'C'}{32,7}=\dfrac{B'C'}{24,3}=\dfrac{10,8}{16,2}\)
=> \(\left\{{}\begin{matrix}A'C'=\dfrac{10,8.32,7}{16,2}=21,8\left(cm\right)\\B'C'=\dfrac{10,8.24,3}{16,2}=16,2\left(cm\right)\end{matrix}\right.\)
Vậy các cạnh của \(\Delta A'B'C'\) có độ dài là :
\(A'B'=10,8cm\)
\(A'C'=21,8cm\)
\(B'C'=16,2cm\)