Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) xét tam giác ( k biết ghi kí hiệu trên này :v) ABC và tam giác HBA có
góc B chung ( kí hiệu góc nhé :D)
góc A = góc BHA = 90 độ ( gt) kí hiệu nhé
Nên tam giác ABC ~ tam giác HBA (g .g) mình ms làm dc câu A thôi :v
TỰ VẼ HÌNH NHA
a) xét tám giác ABC và tam giác HBA
góc A= góc H (=90 độ)
góc A :chung
=> tam giác ABC ~ tam giác HBA (g-g)

B1): a): +)Ta có csc đường cao BD, CE cắt nhau tại I => BD vg góc vs AC; CE vg góc vs AB
+)Xét tg AEC và tg ADB, có: AEC=AHB=90( BD vg góc vs AC; CE vg góc vs AB )
BAC chung
Do đó: tg AEC ~ tg ADB ( gg)
=> AE/AD= AC/AB=> AE*AB=AD*AC (đpcm)
b) : Gợi ý hoi :)): Kẻ đcao AF xuống BC, sẽ đi qua điểm I; c/m ED//BC=> c/m đc tg AED~tg ABC theo trường hợp cgc, từ đó ta sẽ có đc 2 góc AED = ABC ( vì 2 tg trên ~ vs nhau )
A B C 5 5 6 M N
a, Vì BM là phân giác ^B nên : \(\frac{AB}{BC}=\frac{AM}{MC}\)( t/c )
\(\Rightarrow\frac{MC}{BC}=\frac{AM}{AB}\)( tỉ lệ thức )
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{MC}{BC}=\frac{AM}{AB}=\frac{MC+AM}{BC+AB}=\frac{5}{11}\)
\(\Rightarrow\frac{MC}{6}=\frac{5}{11}\Rightarrow MC=\frac{30}{11}\)cm
\(\Rightarrow\frac{AM}{5}=\frac{5}{11}\Rightarrow AM=\frac{25}{11}\)cm

A B C H D
Bài làm:
a) Xét 2 tam giác: \(\Delta ABC\)và \(\Delta HBA\)có:
\(\hept{\begin{cases}\widehat{ABC}chung\\\widehat{AHB}=\widehat{BAC}=90^0\end{cases}}\)
=> \(\Delta ABC\)đồng dang với \(\Delta HBA\)(G.G)
b) \(\Delta AHB\)đồng dạng với \(\Delta CAB\)(G.G) vì:
\(\hept{\begin{cases}\widehat{AHB}=\widehat{AHC}=90^0\\\widehat{BAH}=\widehat{ACH}=90^0-\widehat{HAC}\end{cases}}\)
=> \(\frac{BH}{AH}=\frac{AH}{HC}\)\(\Leftrightarrow AH^2=BH.HC\)
c) Vì tam giác ABC vuông tại A nên theo định lý Py-ta-go, ta có:
\(BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
Theo phần a, \(\Delta ABC\)đồng dạng với \(\Delta HBA\)(G.G)
=> \(\frac{BA}{AH}=\frac{BC}{AC}\Rightarrow AH=\frac{AB.AC}{BC}=\frac{48}{10}=4.8\left(cm\right)\)
Mà theo phần b, \(AH^2=BH.HC\)\(\Leftrightarrow BH.HC=4.8^2=23.04\Leftrightarrow HC=\frac{23.04}{HB}\)
Thay vào ta có: \(HB+HC=BC\)
\(\Leftrightarrow HB+\frac{23.04}{HB}=10\)
Từ đó ta giải phương trình ẩn HB ra, \(HB=3.6\left(cm\right)\)
=> \(HC=10-3.6=6.4\left(cm\right)\)
d) Đề bạn viết nhầm phải là cho AD là phân giác của tam giác ABC.
Áp dụng tính chất của tia phân giác trong tam giác ta có:
\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{3}{4}\Leftrightarrow DC=\frac{4}{3}BD\)
Thay vào đó, ta giải phương trình sau:
\(BD+DC=BC\Leftrightarrow BD+\frac{4}{3}BD=10\)
Từ đó ta giải phương trình ẩn BD => \(BD=\frac{30}{7}cm\)
=> Diện tích tam giác ABD là:
\(S\Delta ABD=\frac{AH.BD}{2}=\frac{4.8\times\frac{30}{7}}{2}=\frac{72}{7}\left(cm^2\right)\)
Học tốt!!!!

1)
A B H D c m n
Kẻ AH là đường cao của ABC
Ta có :\(S_{ABCD}=\frac{1}{2}.AH.BD ; S_{ADC}=\frac{1}{2}.AH.CD\)
\(\Rightarrow\frac{S_{ABC}}{S_{ADC}}=\frac{\frac{1}{2}.AH.BD}{\frac{1}{2}.AH.CD}=\frac{BD}{CD}\left(1\right)\)
\(\Delta ABC\)có AD là tia phân giác
\(\Rightarrow\frac{BD}{CD}=\frac{AB}{AC}\left(2\right)\)
Từ (1)(2)
\(\Rightarrow\frac{S_{ABCD}}{S_{ACD}}=\frac{AB}{AC}=\frac{m}{n}\)
Vậy tỉ số của tam giác ABD và ACD là \(\frac{m}{n}\)

A B C D E 6 H
a) BC = \(\sqrt{AB^2+AC^2}\)= \(\sqrt{6^2+8^2}\)= \(\sqrt{100}\)= 10 (theo định lí Pythagoras)
\(\Delta\)ABC có BD là phân giác => \(\frac{AD}{AB}\)= \(\frac{CD}{BC}\)= \(\frac{AD}{DC}\)= \(\frac{AB}{BC}\)= \(\frac{6}{10}\)= \(\frac{3}{5}\).
b) Ta có : \(\widehat{ABE}\)= \(\widehat{EBC}\)(BD là phân giác)
=> \(\Delta ABD\)~ \(\Delta EBC\)(gg)
=> \(\frac{BD}{BC}\)= \(\frac{AD}{EC}\)<=> BD.EC = AD.BC (đpcm).
c) Ta có : \(\Delta CHE\)~ \(\Delta CEB\)( 2 tam giác vuông có chung góc C )
=> \(\frac{CH}{CE}\)= \(\frac{CE}{CB}\)<=> CH.CB = CE2 (1)
\(\Delta CDE\)~ \(\Delta BDA\)(gg (2 góc đối đỉnh))
\(\Delta BDA~\Delta BCE\) (câu b))
=> \(\Delta CDE~\Delta BCE\)
=> \(\frac{CE}{BE}\)= \(\frac{DE}{CE}\)<=> BE.DE = CE2 (2)
Từ (1) và (2) => CH.CB = ED.EB (đpcm).
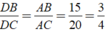
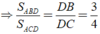
Đường phân giác BACˆ cắt BC tại D
Ta có: DB/DC = AB/AC = 15/20 = 3/4
Chọn đáp án C.