HD
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
14 tháng 11 2019
5b
a)\(\widehat{ADC}>\widehat{ABC}\)
b)\(\widehat{BOC}>\widehat{BAC}\)
7b
Theo định lí tổng ba góc trong 1 tam giác ta có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Mà \(\widehat{B}\)là góc tù => \(\widehat{B}>90^o\)
Tổng 3 góc trg 1 tam giác = 180 độ => A + C = 180 - B
(Giả sử góc B = 80 độ và A = C thì ta có A + C = 180 - 80 = 90 => A = C = 100/2 = 50 độ)
Từ trên suy ra góc A và góc C là 2 góc nhọn
23 tháng 9 2021
a) Ta có: \(2\widehat{B}=7\widehat{C}\Rightarrow\widehat{C}=\dfrac{2}{7}\widehat{B}\)
Ta có: Tam giác ABC vuông tại A
\(\Rightarrow\widehat{B}+\widehat{C}=90^0\)
\(\Rightarrow\widehat{B}+\dfrac{2}{7}\widehat{B}=90^0\)\(\Rightarrow\dfrac{9}{7}\widehat{B}=90^0\Rightarrow\widehat{B}=70^0\)
\(\Rightarrow\widehat{C}=\dfrac{2}{7}\widehat{B}=20^0\)
b) Ta có: AD là phân giác góc A
\(\Rightarrow\widehat{DAC}=\dfrac{1}{2}\widehat{A}=45^0\)
Xét tam giác ADC có:
\(\widehat{ADC}+\widehat{DAC}+\widehat{C}=180^0\)
\(\Rightarrow\widehat{ADC}=180^0-\widehat{DAC}-\widehat{C}=180^0-45^0-20^0=115^0\)
D
1
ND
0
NK
1
16 tháng 9 2017
Đặt \(\widehat{A}=2\widehat{B}=5\widehat{C}=k\)
\(\Rightarrow\hept{\begin{cases}\widehat{A}=k\\\widehat{B}=\frac{k}{2}\\\widehat{C}=\frac{k}{5}\end{cases}}\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=k+\frac{k}{2}+\frac{k}{5}=180^0\)
\(\Rightarrow\frac{17}{10}k=180^0\Leftrightarrow k=\frac{1800}{17}^0\)
\(\Rightarrow\hept{\begin{cases}\widehat{A}=\frac{1800}{17}^0\\\widehat{B}=\frac{900}{17}^0\\\widehat{C}=\frac{360}{17}^0\end{cases}}\)
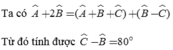
Ta có A=2B=>B=A/2
C=3/2B=>B=2/3C=C/3/2
=>A/2=B=C/3/2 Mà A+B+C=1800
Áp dụng t/c...,ta có:
A/2=B/1=C/3/2=A+B+C/2+1+3/2=1800/9/2=400
+)A/2=400=>A=800
+)B/1=400=>B=400
+)C/3/2=400=>C=600
Vậy A=800
B=400
C=600