Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho tam giác ABC có Â tù. Từ A kẻ AH vuông góc BC. Biết AB=29cm, AC= 40cm, AH= 1/2 BC. Tính BH và HC


góc A = 90 độ
suy ra tam giác ABC vuông tại A.
a) Áp dụng địng lý Pytago trong tam giác vuông ABC ta có: AB2 + AC2 = BC2
Mà AB = 40 cm, AC = 30 cm => BC = 50 cm
b)
Tính AH:
Diện tích tam giác ABC có thể được tính theo hai cách: \(\dfrac{1}{2}\)AB.AC hoặc \(\dfrac{1}{2}\)AH.BC
Suy ra: AH.BC = AB.AC
AH = 40.30:50 = 24 (cm).
Tính BH, CH:
Áp dụng định lý Pytago trong hai tam giác vuông AHB và AHC đều vuông tại H ta được:
+ AH2 + BH2 = AB2 => BH = \(\sqrt{\text{30^2 - 24^2}}\) = 18 (cm)
+ AH2 + CH2 = AC2 => CH = \(\sqrt{\text{40^2 - 24^2}}\) = 32

Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
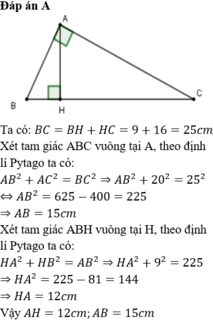
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm

a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là phân giác của góc BAC
=>góc BAH=góc CAH
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
Do đó: ΔADH=ΔAEH
=>AD=AE
=>ΔADE cân tại A

ABCH??20cm16 cm9 cm
Lg
*Áp dụng định lý py-ta-go ta có: (Δ AHC)
AC2=AH2+HC2
202=AH2+162
400=AH2+256
AH2=144
AH=√144 =12
*Áp dụng định lý py-ta-go ta có: (Δ AHB)
AB2=AH2+BH2
AB2=122+92
AB2=225
AB=√225 =15

Đầu tiên bạn vẽ hình trc
- Xét tam giác AHB vuông góc tại H, theo định lý py-ta-go ta có:
AB2=AH2+HB2 hay AB2=122+52=169↔AB=\(\sqrt{169}\)=13 cm
- xét ΔAHC vuông góc tại H, theo đl py-ta-go ta có:
HC2=AC2 - AH2 hay HC2= 152-122=81↔HC=\(\sqrt{81}\)= 9 cm
vậy AB= 13cm và HC= 9cm

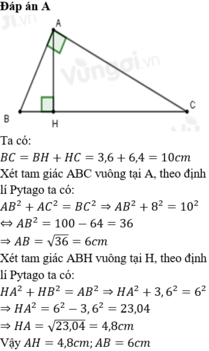
Ap dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=6^2+8^2=100\)
\(\Leftrightarrow\)\(BC=\sqrt{100}=10\)
Ta có hình vẽ: A H B C
Áp dụng định lý Pitago. Ta có:
BC2 = AB2 + AC2 <=> 62 + 82 = 100 cm2
100 = 10 x 10
=> BC = 10 cm
Áp dụng công thức Heron để tính chiều cao. Ta có:
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) (p là chu vi, S là diện tích, a,b,c là độ dài 3 cạnh)
Ta có: Chu vi tam giác là: 6 + 8 + 10 =24 cm
Vậy \(S=\sqrt{24\left(24-6\right)\left(24-8\right)\left(24-10\right)}=48\sqrt{42}\)
Để tính chiều cao AH, ta lấy 2 lần diện tích chia cho đáy ( BC) sẽ có được chiều cao
2 lần diện tích là: \(48\sqrt{42}.2=96\sqrt{42}\)
\(\Rightarrow AH=96\sqrt{42}:10=\frac{24\sqrt{42}}{25}\)
Độ dài cạnh BH là: (Bạn tự làm)
Độ dài cạnh HC là: (Bạn tự làm nhé)
sai số liệu
đúng rồi bạn