Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vẽ hình
a xét tam giác ABD và tam giác ACE có :
chung góc BAC
góc BDA = góc CEA = 90 độ
=> tam giác ABD đồng dạng tam giác ACE (g.g)
b, xét tam giác EHB và tam giác DHC có
góc BDC = góc CFB = 90 độ
góc BHF = góc DHC ( đối đỉnh )
=> tam giác EHB đồng dạng với tam giác DHC (g.g)
=> \(\frac{HB}{HC}=\frac{HE}{HD}\)
=> HD . HB = HE . HC ( đpcm )
c, vì tam giác ABD đồng dạng với tam giác ACE ( câu a)
=> \(\frac{AB}{AC}=\frac{AD}{AE}\) => \(\frac{AE}{AC}=\frac{AD}{AB}\)
xét tam giác ADE và tam giác ABC có
chung góc BAC
\(\frac{AE}{AC}=\frac{AD}{AB}\)
=> tam giác ADE đồng dạng với tam giác ABC ( c.g.c)
=> góc ADE = góc ABC ( đpcm)

a, Xét Δ ABD và Δ ABE, có :
\(\widehat{ADB}=\widehat{AEB}=90^o\)
\(\widehat{BAD}=\widehat{BAE}\) (góc chung)
=> Δ ABD ∾ Δ ABE (g.g)
b, Xét Δ EHB và Δ DHC, có :
\(\widehat{EHB}=\widehat{DHC}\) (đối đỉnh)
\(\widehat{HEB}=\widehat{HDC}=90^o\)
=> Δ EHB ∾ Δ DHC (g.g)
=> \(\dfrac{EH}{DH}=\dfrac{HB}{HC}\)
=> \(HB.HD=HC.HE\)

a) Có góc A chung và 2 góc vuông => ĐPCM
b) Xét EHB và DHC có:
2 góc vuông và 2 góc đối đỉnh EHB và DHC
=> EHB đồng dạng với DHC
=>BH/CH=EH/DH
=>BH.DH=EH.CH
c)Từ câu a ta suy ra được tỉ số : AB/AC=AD/AE
và có góc A chung .
Từ đó suy ra: ADE đồng dạng với ABC
=> góc ADE= góc ABC
d) Ta có IO là đường trung bình ( tự chứng minh )
=> IO//AH => AHM đồng dạng với IOM
Tỉ số cạnh = AM/IM =2 ( do là đường trung bình )
Tỉ số diện tích của AHM so với IOM là 22=4
Vậy SAHM=4.SIOM

A B C D E
\(\Delta ACE\)vuông tại A có \(\widehat{A}=60^o\)nên \(\widehat{ACE}=30^o\)
\(\Rightarrow\frac{AE}{AC}=\frac{1}{2}\)
Tương tự : \(\frac{AD}{AB}=\frac{1}{2}\)
\(\Rightarrow\frac{AE}{AC}=\frac{AD}{AB}\Rightarrow\frac{AE}{AD}=\frac{AC}{AB}\)
chứng minh : \(\Delta ADE\approx\Delta ABC\)( c.g.c )
\(\Rightarrow\frac{S_{ADE}}{S_{ABC}}=\left(\frac{AD}{AB}\right)^2=\frac{1}{4}\)
\(\Rightarrow S_{ADE}=\frac{1}{4}S_{ABC}\)

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
b: Xet ΔHEB vuôg tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HB*HD
c: ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD/AB=AE/AC
=>ΔADE đồng dạng với ΔABC
=>góc ADE=góc ABC
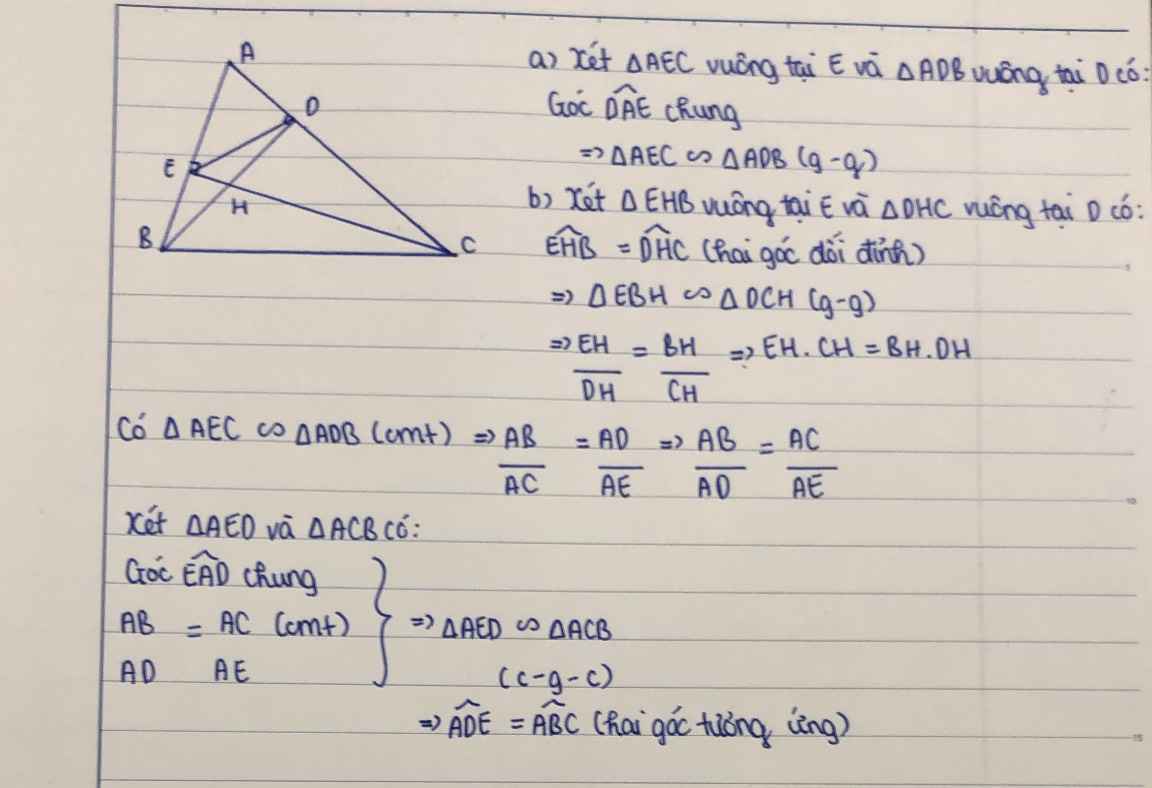

Tam giác ADE và tg ABC có
\(\hept{\begin{cases}\widehat{A}chung\\\\\frac{AD}{AE}=\frac{AB}{AC}\left(\frac{AD}{AB}=\cos\widehat{A}=\frac{AE}{AC}\right)\end{cases}}\)
Suy ra ADE đồng dạng ABC
=> đpcm
sorry mk ch hojccasi này