Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GIẢI: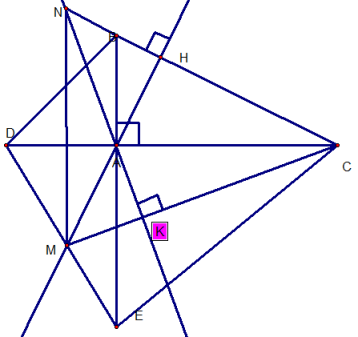
a) Xét Δ ABC và Δ AED, ta có :
(đối đỉnh)
AB = AD (gt)
AC = AD (gt)
=> Δ ABC = Δ AED (hai cạnh góc vuông)
=> BC = DE
Xét Δ ABD, ta có :
(Δ ABC vuông tại A)
=> AD AE
=>
=> Δ ABD vuông tại A.
mà : AB = AD (gt)
=> Δ ABD vuông cân tại A.
=>
cmtt :
=>
mà : ở vị trí so le trong
=> BD // CE
b) Xét Δ MNC, ta có :
NK MC = > NK là đường cao thứ 1.
MH NC = > MH là đường cao thứ 2.
NK cắt MH tại A.
=> A là trực tâm. = > CA là đường cao thứ 3.
=> MN AC tại I.
mà : AB AC
=> MN // AB.
c) Xét Δ AMC, ta có :
(đối đỉnh)
(Δ ABC = Δ AED)
=> (cùng phụ góc ABC)
=> Δ AMC cân tại M
=> AM = ME (1)
Xét Δ AMI và Δ DMI, ta có :
(MN
AC tại I)
IM cạnh chung.
mặt khác : (so le trong)
(đồng vị)
mà : (cmt)
=>
=> Δ AMI = Δ DMI (góc nhọn – cạnh góc vuông)
=> MA = MD (2)
từ (1) và (2), suy ta : MA = ME = MD
ta lại có : ME = MD = DE/2 (D, M, E thẳng hàng)
=>MA = DE/2.

bạn vô đây coi bài nào thích hớp thì xem Cho tam giác ABC. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Gọi H là chân đường vuông góc kể từ B đến AD, K là chân đường vuông góc kẻ từ C đến AE a) Chứng minh rằng HK song song với DE b) Tính HK, biết chu vi tam giác ABC bằng 10 cm Bài 2 Cho tam giác ABC, đường trung tuyến AM. Trên tia đối của tia AM lấy điểm N sao cho AN = AM. Gọi K là giao điểm của CA và NB. Chứng minh NK = 1/2 KB... Xem thêm - Tìm với Google

a: góc ADH+góc AEH=180 độ
=>ADHE nội tiếp
O là trung điểm của AH
b:
XetΔACB có
BD,CE là đường cao
BD căt CE tại H
=>H là trực tâm
=>AH vuông góc BC
=>K là trung điểm của CB
góc ODK=góc ODH+góc KDH
=góc BHK+góc KBH=90 độ
=>KD là tiếp tuyến của (O)

Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).
ABCDEMI
Từ D kẻ DI // AE
Vì ΔΔABC cân tại A nên BˆB^ = ACBˆACB^ (1)
Vì DI // AE => ACBˆACB^ = DIBˆDIB^ (đồng vị ) (2)
Từ (1) và (2) => BˆB^ = DIBˆDIB^
Trong ΔΔDIB có : BˆB^ = DIBˆDIB^ => ΔΔDIB cân tại D
=> DB = DI mà DB = CE (gt)
=> DI = CE
Vì DI // AE => MDIˆMDI^ = MECˆMEC^(so le trong )
và DIMˆDIM^ = MCEˆMCE^ ( so le trong )
Xét ΔΔDIM và ΔΔECM có :
MDIˆMDI^ = MECˆMEC^ (chứng minh trên )
đăng từ năm ngoái năm nay moi trả lời