Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chắc là bạn sai đề rồi
tam giác ABC mà góc A = 90 độ thì sao mà kẻ BD vuông góc với AC tại D, CE vuông góc với AB tại E được

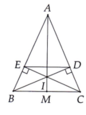
a) Xét ΔAEC vuông tại E và ΔADB vuông tại D có
AC=AB(ΔABC cân tại A)
\(\widehat{BAD}\) chung
Do đó: ΔAEC=ΔADB(cạnh huyền-góc nhọn)
Suy ra: AE=AD(hai cạnh tương ứng)
Xét ΔAED có AE=AD(cmt)
nên ΔAED cân tại A(Định nghĩa tam giác cân)

Bài 2:
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔADB=ΔAEC
Suy ra: AD=AE
hayΔADE cân tại A
b: Xét ΔABC có
AE/AB=AD/AC
nên DE//BC
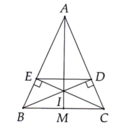
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
EC=DB
BC chung
Do đó: ΔEBC=ΔDCB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
hay ΔIBC cân tại I
d: Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
Do đó: ΔAEI=ΔADI
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
=>AK là tia phân giác của góc BAC
Ta có: ΔABC cân tại A
mà AK là đường phân giác
nên AK là đường cao