Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


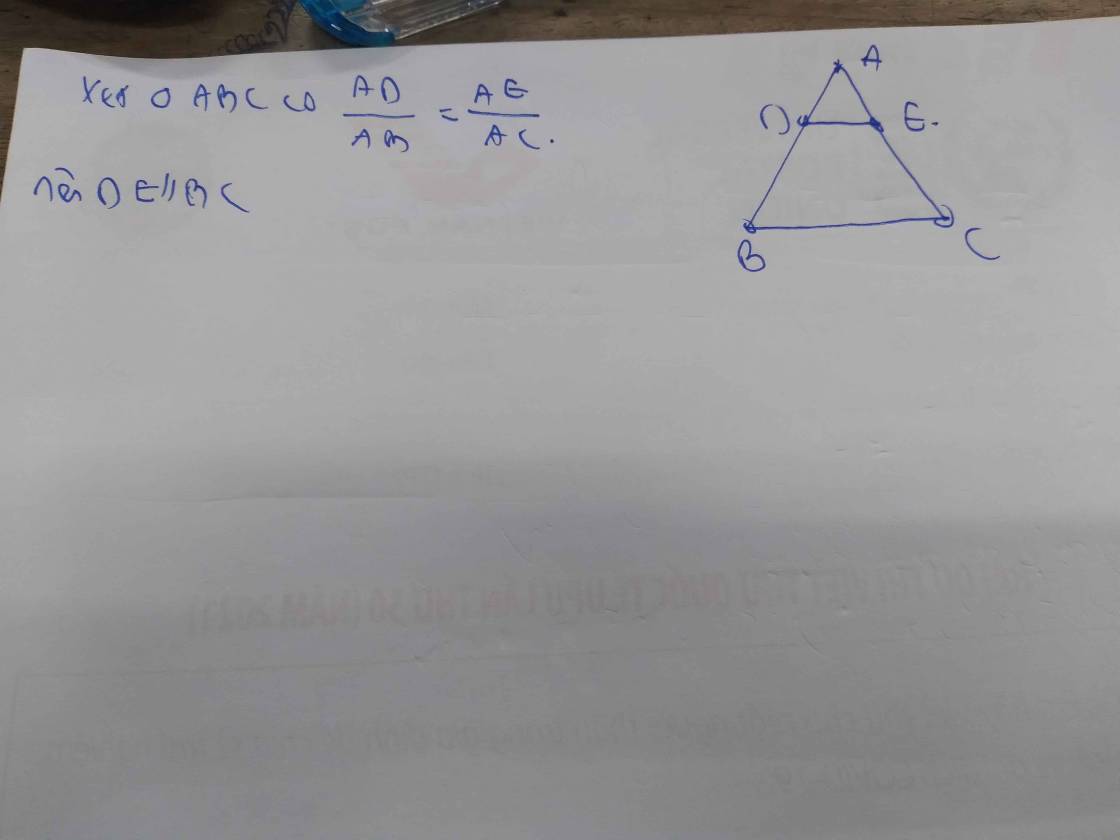
Ta có :góc DAE=góc BAC (đối đỉnh)
Xét tam giác ABC cân tại A : \(ABC=ACB=\frac{180^0-BAC}{2}\)
Xét tam giác DAE cân tại A: \(ADE=AED=\frac{180^0-DAE}{2}\)
=>góc ABC=góc ACB=góc ADE=góc AED
Vì góc ADE=góc ACB,mà chúng ở vị trí SLT
=>DE//BC
=>tg BEDC là hình thang
Xét tam giác DAB và tam giác EAC :
góc DAB=góc EAC (đối đỉnh)
AD=AE(gt)
AB=AC(tam giác ABC cân tại A)
=>tg DAB=tg EAC (c.g.c)
=>BD=EC (cặp cạnh t.ứng)
Vì ht BEDC có BD=EC
=>BEDC là hình thang cân

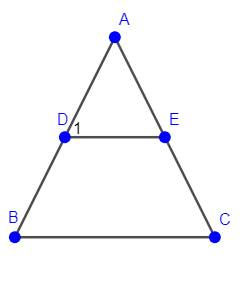
Có `Delta ABC` cân tại `A(GT)=>hat(B)=(180^0-hat(A))/2` (1)
`AD=AE=>Delta AED` cân tại `A=>hat(D_1)=(180^0-hat(A))/2` (2)
Từ `(1);(2)=>hat(B)=hat(D_1)`
mà `2` góc này ở vị trí đvị
nên `DE////BC(đpcm)`

Đáp án cần chọn là: C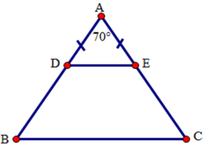
Tam giác ADE có AD = AE (gt) nen tam giác ADE cân tại A.
Suy ra A D E ^ = A E D ^ = 180 ° - D A E ^ ÷ 2 (1)
Tam giác ABC cân tại A (gt) nên A B C ^ = A C B ^ = 180 ° - B A C ^ ÷ 2 (2)
Từ (1) và (2) suy ra A D E ^ = A B C ^
Mà 2 góc và là hai góc ở vị trí đồng vị nên suy ra DE // BC
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang
Lại có A B C ^ = A C B ^ (vì tam giác ABC cân tại A) nên BDEC là hình thang cân