Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) dùng 2 góc đồng vị (góc B với M hoặc góc C với N)
2) cm 2 góc BAE và CAE bằng nhau
suy ra tam giác BAE = tam giác CAE
suy ra AB = AC; EB = EC
nên AE là đường trung trực của BC
suy ra AE vuông góc với BC
cm AI vuông gõ với BC suy ra A,I, E thẳng hàng

Bài 5:
Tgiac ABC vuông cân tại A => góc CBA = 45 độ
Xét góc CBA là góc ngoài tgiac DBC => góc CBA = góc D + DCB
Xét tgiac DBC có DB = BC => tgiac DBC cân tại B => góc D = góc DBC
=> góc D = 45/2 = 22,5 độ
và góc ACD = 22,5 + 45 = 67,5 độ
Vậy số đo các góc của tgiac ACD là ...
Bài 6:
Tgiac ABC cân tại B, góc B = 100 độ => góc A = góc C = 40 độ
Xét tgiac ABD có AB = AD => tgiac ABD cân tại A => góc EDB (ADB) = (180-40)/2 =70 độ
cmtt với tgiac CBE => góc DEB = 70 độ
=> góc DBE = 180-70-70 = 40 độ
Bài 7:
Xét tgiac ABC cân tại A => góc BAC = 180 - 2.góc C => 2.(90 - góc C)
Xét tgiac BHC vuông tại H => góc CBH = 90 - góc C
=> đpcm
Bài 8: mai làm hihi

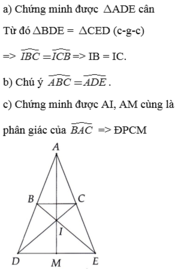
Xét ΔABM và ΔACM có:
AB = AC ( giả thiết)
BM = CM ( vì M là trung điểm BC )
AM chung
⇒ ΔABM = ΔACM (c.c.c)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180o
⇒ ∠AMB = ∠AMC = 90o hay AM ⊥ BC
Chứng minh tương tự ta có: IM ⊥ BC
⇒ A, I, M thẳng hàng (Qua 1 điểm ta kẻ được duy nhất 1 đường thẳng vuông góc với đường thẳng cho trước)
Hình bạn tự vẽ nha :))
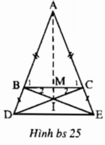
a)* Ta có: \(\Delta ABC\)cân tại A <=> AB=AC
\(\hept{\begin{cases}AM=AB+MB\\AN=AC+NC\end{cases}\Rightarrow AM=AN}\)(do \(AB=AC;MB=NC\))
\(\Rightarrow\Delta AMN\)cân tại A
* Từ \(\Delta ABC\)cân tại A, có: \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\)(1)
Từ \(\Delta AMN\)cân tại A, có: \(\widehat{AMN}=\frac{180^o-\widehat{A}}{2}\)(2)
Từ (1) và (2), suy ra: \(\widehat{ABC}=\widehat{AMN}\)
\(\Rightarrow MN//BC\)(2 góc đồng vị bằng nhau)
b) Xét \(\Delta ABI\)và \(\Delta ACI\)có:
\(\hept{\begin{cases}AB=AC\\AIchung\\IB=IC\end{cases}\Rightarrow\Delta ABI=\Delta}ACI\left(ccc\right)\)
\(\Rightarrow\widehat{BAI}=\widehat{CAI}\)(2 góc tương ứng)
\(\Rightarrow AI\)là p/giác của \(B\widehat{A}C\) (3)
Tương tự, ta có: \(\widehat{MAE}=\widehat{NAE}\)
\(\Rightarrow AE\)là p/ giác của \(\widehat{BAC}\)(4)
Từ (3) và (4), ta có: A,I,E thẳng hàng