Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác AKCI co
M là trung điểm chung của AC và KI
nên AKCI là hình bình hành
=>CI//AK

a: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
BC chung
=>ΔNBC=ΔMCB
b: ΔNBC=ΔMCB
=>góc KBC=góc KCB
=>ΔKBC cân tại K
c: Xét tứ giácc AKCI có
M là trung điểm chung của AC và KI
nên AKCI là hình bình hành
=>CI//AK

a, Do \(NA=NB=\frac{1}{2}AB\)
\(AM=MC=\frac{1}{2}AC\)
Mà \(AB=AC\)\(\Rightarrow NA=MA;NB=MC\)\(\Rightarrow\)\(\Delta AMN\)cân tại \(A\)
b, Xét \(\Delta ANC\)và \(\Delta AMB\)có:
\(\widehat{BAC}chung\)
\(AB=AC\)
\(AN=AM\)(câu a)
\(\Rightarrow\Delta ANC=\Delta AMB\)
\(\Rightarrow BM=CN\)
c, Xét \(\Delta NBC\) và\(\Delta MCB\) có:
\(BCchung\)
NB = MC ( câu a)
NC = MB ( câu b)
=>\(\Delta NBC=\Delta MCB\)=>\(\widehat{GBC}=\widehat{GCB}\)=>\(\Delta GBC\) cân tại C
TYM cho chị nhé <3

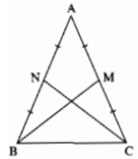
Ta có hình vẽ:
A B C N M
Theo bài ra ta có:
Tam giác ABC cân tại A
=> AB=AC ( hai cạnh bên của tam giác cân )
Ta lại có:
M là trung điểm của AC;N là trung điểm của AB
=> AN=BN=CM=AM
Ta có: \(\Delta ABM=\Delta ACN\) (c.g.c)
=> BM=CN ( hai cạnh tuơng ứng )
(đ.p.c.m)

\(\hept{\begin{cases}AB=AC\\AM=\frac{1}{2}AC\\AN=\frac{1}{2}AB\end{cases}}\)
Từ đó suy ra AM=AN
=>BM=CN
ta có tam giác ABC cân tại A => AB=AC ( hai cạnh bên)
mà ta có AM =MC (vì m là trung điểm) => mc=\(\frac{1}{2}ac\)
ta lại có an =nb (vì n là trung điểm ab)=> nb=\(\frac{1}{2}ab\) mà ab=ac=> 1/2 ab=1/2ac hay mc=bn
xét tam giác bnc và tam giác cmb có:
bn=mc(cmt)
góc nbc=góc mcb
bc chung
do đó tam giác bnc = tam giác cmb (c.g.c)
=>nc=bm (hai cạnh tương ứng)
thông cảm hình vẽ quá xấu mình chắc chắn đúng đó

+) Do M là trung điểm của AC nên: 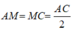 (1)
(1)
+) Do N là trung điểm của AB nên: 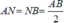 (2)
(2)
Lại có: AB = AC ( vì tam giác ABC cân tại A). (3)
Từ (1); (2); (3) suy ra: AN = NB = AM = MC.
+) Xét ∆ AMB và ∆ANC có:
Góc A chung
AM = AN ( chứng minh trên)
AB = AC ( vì tam giác ABC cân tại A)
Suy ra: ∆ AMB = ∆ANC ( c.g.c)
Do đó: BM = CN ( hai cạnh tương ứng).

Ta có: AN = BN = \(\dfrac{1}{2}\)AB (N là trung điểm của AB)
AM = CM = \(\dfrac{1}{2}\)AC (M là trung điểm của AC)
Mà AB = AC ( do tam giác ABC cân tại A)
=> AN = BN = AM = CM
Xét tam giác BNC và tam giác CMB:
+ BC chung
+ ^B = ^C (tam giác ABC cân tại A)
+ BN = CM (cmt)
=> Tam giác BNC = tam giác CMB (c-g-c)
=> ^NCB = ^MBC (2 góc tương ứng)
Hay ^KCB = ^KBC
=> Tam giác BKC cân tai K
Xét tam giác ABC: M là trung điểm của AC (gt)
N là trung điểm của AB (gt)
=> MN là đường trung bình của tam giác ABC (định nghĩa đường trung bình trong tam giác)
=> MN // BC (TC đường trung bình trong tam giác)
a) Ta có: \(AN=NB=\dfrac{AB}{2}\)(N là trung điểm của AB)
\(AM=MC=\dfrac{AC}{2}\)(M là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AN=NB=AM=MC
Xét ΔBNC và ΔCMB có
BN=CM(cmt)
\(\widehat{NBC}=\widehat{MCB}\)(hai góc ở đáy của ΔABC cân tại A)
BC chung
Do đó: ΔBNC=ΔCMB(c-g-c)
b) Xét ΔANC và ΔABM có
AN=AM(cmt)
\(\widehat{NAC}\) chung
AC=AB(ΔABC cân tại A)
Do đó: ΔANC=ΔABM(c-g-c)
⇒\(\widehat{ACN}=\widehat{ABM}\)(hai góc tương ứng)
hay \(\widehat{NBK}=\widehat{MCK}\)
Xét ΔNBK có
\(\widehat{NBK}+\widehat{NKB}+\widehat{BNK}=180^0\)(Định lí tổng ba góc trong một tam giác)(1)
Xét ΔMCK có
\(\widehat{MCK}+\widehat{MKC}+\widehat{CMK}=180^0\)(Định lí tổng ba góc trong một tam giác)(2)
Từ (1) và (2) suy ra \(\widehat{NBK}+\widehat{NKB}+\widehat{BNK}=\widehat{MCK}+\widehat{MKC}+\widehat{CMK}\)
mà \(\widehat{NBK}=\widehat{MCK}\)(cmt)
và \(\widehat{NKB}=\widehat{MKC}\)(hai góc đối đỉnh)nên \(\widehat{BNK}=\widehat{CMK}\)Xét ΔNBK và ΔMCK có \(\widehat{BNK}=\widehat{CMK}\)(cmt)BN=CM(cmt)\(\widehat{NBK}=\widehat{MCK}\)(cmt)Do đó: ΔNBK=ΔMCK(g-c-g)⇒KB=KC(hai cạnh tương ứng)Xét ΔKBC có KB=KC(cmt)nên ΔKBC cân tại K(Định nghĩa tam giác cân)
Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
BC chung
=>ΔNBC=ΔMCB
=>góc KBC=góc KCB
=>ΔKBC cân tại K