Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu này mình vừa làm ở bạn Khang Phạm Duy , HÂN nhé
tham khảo .mình giải rất chi tiết

a, theo pytago ta có:
AB2+AC2=BC2 <=> AC=\(\sqrt{10^2-6^2}\)=8 (cm)
so sánh: BAC>ABC>ACB vì BC>AC>AB
b, vì A là trung điểm BD nên CA là trung tuyến của tam giác DBC
mà CA\(\perp\)BD nên CA là đường cao của tam giác DBC
=> CA vừa là trung tuyến vừa là đường cao của tam giác DBC nên DBC cân ở C

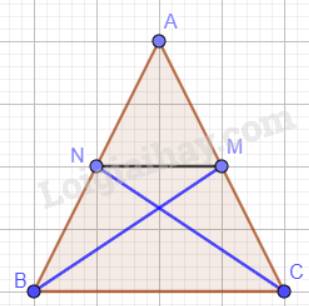
Tam giác ABC cân tại A nên AB = AC.
M và N lần lượt là trung điểm của AC và AB nên:
\(\begin{array}{l}AN = BN = \dfrac{1}{2}AB\\AM = CM = \dfrac{1}{2}AC\end{array}\)
Mà AB = AC nên AN = BN = AM = CM.
Xét tam giác AMB và tam giác ANC có:
\(\widehat A\)chung;
AB = AC (cmt);
AM = AN (cmt).
Vậy \(\Delta AMB = \Delta ANC\)(c.g.c) nên BM = CN ( 2 cạnh tương ứng).

a) tam giác ABC vuông tại A
=> AB2 + AC2 = BC2 (định lý py-ta-go)
=> 92 + AC2 = 152
=> AC2 = 225 - 81
=> AC2 = 144 => AC = \(\sqrt{144}=12cm\)
t i c k đúng nhé
a) trong tam giác ABC có: AB < AC < BC ( 9 < 12 < 15)
=> góc C < góc B < góc A (định lý)
Để chứng minh rằng \( BM = CN \), chúng ta sẽ sử dụng tính chất của tam giác cân.
Vì tam giác \( ABC \) cân tại \( A \), nên ta có \( AM = MC \) và \( AN = NB \), vì \( M \) là trung điểm của \( AC \) và \( N \) là trung điểm của \( AB \).
Bây giờ, ta cần chứng minh \( BM = CN \).
Ta có thể sử dụng định lí đối xứng của tam giác để chứng minh điều này.
Xét tam giác \( AMC \) và \( ANB \):
- \( AM = MC \) (vì \( M \) là trung điểm của \( AC \))
- \( AN = NB \) (vì \( N \) là trung điểm của \( AB \))
- \( AC = AB \) (vì tam giác \( ABC \) cân tại \( A \))
Theo định lí đối xứng của tam giác, ta có \( BM = CN \), vì hai tam giác \( AMC \) và \( ANB \) là đối xứng với nhau qua đường trung tuyến \( MN \).
Do đó, \( BM = CN \).
sai rồi