Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

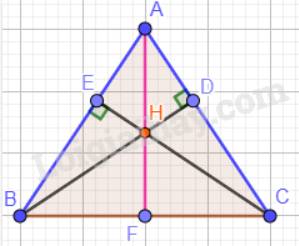
a) Tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB} = 70^\circ \).
Tổng ba góc trong một tam giác bằng 180° nên: \(\widehat {BAC} = 180^\circ - 70^\circ - 70^\circ = 40^\circ \).
b) Xét tam giác vuông ADB và tam giác vuông AEC có:
AB = AC (tam giác ABC cân);
\(\widehat A\) chung.
Vậy \(\Delta ADB = \Delta AEC\)(cạnh huyền – góc nhọn). Suy ra: BD = CE ( 2 cạnh tương ứng).
c) Trong tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm trong tam giác ABC hay AF vuông góc với BC.
Xét hai tam giác vuông AFB và AFC có:
AB = AC (tam giác ABC cân);
AF chung.
Vậy \(\Delta AFB = \Delta AFC\)(cạnh huyền – cạnh góc vuông). Suy ra: \(\widehat {FAB} = \widehat {FAC}\) ( 2 góc tương ứng) hay \(\widehat {BAH} = \widehat {CAH}\).
Vậy tia AH là tia phân giác của góc BAC.

a: góc ABC=góc ACB=(180-50)/2=65 độ
b: Xét ΔAMB và ΔANC có
AM=AN
góc BAM chung
AB=AC
=>ΔAMB=ΔANC

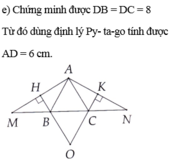
a: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
=>\(\widehat{ACB}=50^0\)
ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ABC}=180^0-2\cdot50^0=80^0\)
b: Xét ΔNBC vuông tại N và ΔMCB vuông tại M có
BC chung
\(\widehat{NBC}=\widehat{MCB}\)(ΔABC cân tại A)
Do đó: ΔNBC=ΔMCB
=>CN=MB
c: ΔNBC=ΔMCB
=>\(\widehat{NCB}=\widehat{MBC}\)
=>\(\widehat{HBC}=\widehat{HCB}\)
=>ΔHBC cân tại H
Xét ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
Do đó: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
a) ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB = 50⁰
∠ABC + ∠ACB + ∠BAC = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠BAC = 180⁰ - (∠ABC + ∠ACB)
= 180⁰ - (50⁰ + 50⁰)
= 80⁰
b) Ta có:
∠ABC = ∠ACB (cmt)
⇒ ∠NBC = ∠MCB
Xét hai tam giác vuông: ∆NBC và ∆MCB có:
BC là cạnh chung
∠NBC = ∠MCB (cmt)
⇒ ∆NBC = ∆MCB (cạnh huyền - góc nhọn)
⇒ CN = BM (hai cạnh tương ứng)
Hay BM = CN
c) ∆ABC cân tại A (gt)
BM là đường cao (gt)
CN là đường cao thứ hai (gt)
⇒ AH là đường cao thứ ba
⇒ AH cũng là đường phân giác
⇒ AH là tia phân giác của ∠BAC