Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, + Xét tg HBG và tg HCG vuông tại H
Có : HG cạnh chung
Mà : AH là đường cao trong tg cân nên :
AH là đường trung tuyến và là đường fan giác
=> BH=HC (vì AH là đường trung tuyến)
Nên: tg HBG=HCG (ch-cgv)
Vậy : BG=GC ( 2 cạnh tương ứng ) (1)
+ Xét tg BHE và tg HCE vuông tại H
Có : HE cạnh chung
BH=HC
Nên : tg BHE= tg HCE (ch-cgv)
Vậy : BE=EC (2 cạnh tương ứng ) (2)
+Xét tg HGC và tg HCE vuông tại H
Có : HC cạnh chung
HG=HE
Nên : tg HGC=tg HCE
Vậy : GC=ce (2 cạnh tương ứng) (3)
+Xét tg BHG và tg BHE vuông tại H
BH cạnh chung
HG=HE
nên : tg BHG = tg BHE
Vậy : BG=BE ( 2 cạnh tương ứng ) (4)
Từ (1)(2)(3) và (4) suy ra :BG=CG=BE=CE
b,Xét tg ABE và tg ACE
Có : AB= AC ( tg ABC cân tại A)
BE=EC( cmt)
AE cạnh chung
Vậy : tg ABE = tg ACE (ccc)
c, k bt
d, k bt
e, Trong tg GBE có :
BG=BE
Mà trong tam giác có 2 cạnh bằng nhau thì tg đó là tg cân hoặc đều
Nên : tg GBE là tg đều .
Vậy : đpcm

a: Xét tứ giác BGCE có
H là trung điểm của BC
H là trung điểm của GE
Do đó; BGCE là hình bình hành
mà GE⊥CB
nên BGCE là hình thoi
=>BG=GC=CE=BE
b: Ta có: AG=2GH
mà GE=2GH
nên GA=GE
c: BC=8cm nên BH=4(cm)
\(AB=\sqrt{9^2+4^2}=\sqrt{97}\left(cm\right)\)

1.
a) Xét ΔADE có :
HE là đường trung tuyến của AD HA=HD )(1)
Ta thấy HC=12BC ( AH là đường trung tuyến của BC )
Mà BC = CE (gt )
⇒HC=12CE (2)
Từ (1) và (2) ⇒C là trọng tâm của ΔADE
b) Hơi khó đấy :)
Xét ΔAHB và ΔAHC có :
HAHA chung
HB=HC ( AH là đường trung tuyến của BC )
AB=AC( ΔABC cân tại A )
Do đó : ΔAHB=ΔAHC(c−c−c)
⇒AHBˆ=AHCˆ( hai góc tương ứng )
Mà AHBˆ+AHCˆ=1800
⇒AHB^=AHC^=1800/2=90o
Xét ΔAHEvà ΔHED có :
HEHE chung
HA=HD( HE là đường trung tuyến của AD )
AHEˆ=DHEˆ(=900)
Do đó : ΔAHE=ΔDHE ( hai cạnh góc vuông )
⇒AEHˆ=DEHˆ ( góc tương ứng ) (*)
Vì C là trọng tâm của ΔAED là đường trung tuyến của DE )
Xét vuông tại H có : HM là đường trung tuyến nối từ đỉnh H đến DE
⇒HM=DM (1)
Lưu ý : Trong tam giác vuông , đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền . Tức HM=12DE Mà 12DE=DM⇒HM=DM
Trở lại vào bài :
Mặt khác DM=ME(cmt)(2)
Từ (1) và (2) ⇒HM=ME
⇒ΔHME⇒ΔHME cân tại M
⇒MHEˆ=MEHˆ
Dễ thấy MEHˆ=HEAˆ(cmt)
⇒MHEˆ=HEAˆ
mà hai góc này ở vị trí so le trong
⇒HM⇒HM//AE(đpcm)
2.
a) ta có: \(\Delta OAB,\Delta OAC\) có diện tích bằng nhau và cùng đáy OA nên khoảng cách từ B , C kẻ đến OA
nên BH=CK
b) gọi AK giao với BC tại M
Xét \(\Delta BHM\)và \(\Delta CKM\) có:
..........
3.
a. xét tgiac ADC và tgiac ADB có
AD là cạnh chung
góc DAB = góc DAC(gt)
AB=AC(gt)
vậy tg ADC=tg ADB(c.g.c)
b.theo cminh cau a ta có DB=DC(2 cạnh tương ứng)
nên AD là đường trung tuyến ứng với cạnh BC mà G là trọng tâm tâm giác ABC nên A D G thẳng hàng
k mk nha thack ae
Bài 1 :
a) Vì AH = HD => EH là đg trung tuyến của tg ADE
Khi đó C thuộc đg trung tuyến EH (1)
Do tam giác ABC cân tại A
mà AH là đường cao của tam giác ABC
=> AH là đg trung trực của tam giác ABC
=> BH = CH
=> BH = CH = \(\frac{1}{2}\)BC
Lại do BC = CE
=> CH = \(\frac{1}{2}\) CE
hay CE = \(\frac{2}{3}\) EH (2)
Từ (1); (2) => C là trọng tâm của tam giác ADE.
b) Có : AH là đường cao của ΔABC
⇒ Góc AHC = 90
⇒ Góc DHC = 90 (kề bù)
Xét ΔAHE và ΔDHE có:
+ AH = DH (gt)
+ Góc AHE = góc DHE = 90
+ HE chung
⇒ ΔAHE = ΔDHE
⇒ Góc EAH = góc EDH (1)
Lại có: Tia AC cắt DE tại M
Mà C là trong tâm của ΔADE
⇒ AM là trung tuyến của ΔADE
⇒ M là trung điểm của DE
Mà ΔDHE là tam giác vuông tại H (do DHE = 90 )
⇒ HM là đường trung tuyến của cạnh huyền
⇒ HM = DM = EM
⇒ ΔHMD cân tại M
⇒ Góc MHD = góc MDH (2)
Từ (1) + (2) ⇒ Góc EAH = góc MHD
Mà hai góc này là hai góc đồng vị
⇒ AE // HM (đpcm)

a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của CB
=>CB=2CH
mà CB=CE
nên CE=2CH
=>\(\dfrac{EC}{EH}=\dfrac{2}{3}\)
Xét ΔEAD có
EH là đường trung tuyến
\(EC=\dfrac{2}{3}EH\)
Do đó: C là trọng tâm của ΔEAD
b: Xét ΔEAD có
C là trọng tâm
AC cắt DE tại M
Do đó: M là trung điểm của DE
Xét ΔEAD có
H,M lần lượt là trung điểm của DA,DE
=>HM là đường trung bình của ΔEAD
=>HM//AE
c: Để HM\(\perp\)AB thì AE\(\perp\)AB
=>ΔABE vuông tại A
Ta có: ΔABE vuông tại A
mà AC là đường trung tuyến
nên AC=CB=CE
=>AC=CB
mà AB=AC
nên AC=AB=BC
=>ΔABC đều
=>\(\widehat{ABC}=60^0\)
Khi ΔABC đều thì \(\widehat{HAC}=\dfrac{60^0}{2}=30^0\)
Ta có: \(\widehat{ACE}+\widehat{ACB}=180^0\)(hai góc kề bù)
=>\(\widehat{ACE}+60^0=180^0\)
=>\(\widehat{ACE}=120^0\)
Ta có: CA=CE
=>ΔCAE cân tại C
=>\(\widehat{CAE}=\widehat{CEA}=\dfrac{180^0-\widehat{ACE}}{2}=30^0\)
\(\widehat{HAE}=\widehat{HAC}+\widehat{CAE}=30^0+30^0=60^0\)
Xét ΔEAD có
EH là đường cao
EH là đường trung tuyến
Do đó: ΔEAD cân tại E
mà \(\widehat{EAD}=60^0\)
nên ΔEAD đều
Ta có: ΔABC đều
mà AH là đường cao
nên \(AH=AB\cdot\dfrac{\sqrt{3}}{2}=\dfrac{3\sqrt{3}}{2}\left(cm\right)\)
H là trung điểm của AD
=>\(AD=2\cdot AH=3\sqrt{3}\left(cm\right)\)
ΔADE đều
mà AM là đường trung tuyến
nên AM\(\perp\)DE
=>ΔAMD vuông tại M
Xét ΔAMD vuông tại M có \(cosDAM=\dfrac{AM}{AD}\)
=>\(\dfrac{AM}{3\sqrt{3}}=cos30=\dfrac{\sqrt{3}}{2}\)
=>\(AM=4,5\left(cm\right)\)

Bài 1)
a) Trong ∆ cân ABC có AH là trung trực đồng thời là phân giác và trung tuyến
=> BAH = CAH
Xét ∆ ABD và ∆ ACD ta có :
AB = AC (∆ABC cân tại A)
AD chung
BAH = CAH (cmt)
=> ∆ABD = ∆ACD (c.g.c)
=> BD = CD
=> ∆BDC cân tại D
* NOTE : Trong ∆ vuông BDH có DH < BD ( trong tam giác vuông ; cạnh góc vuông luôn luôn nhỏ hơn cạnh huyền )
Mà DH = HG
=> DG < DB
=> DG ko thể = BD và DC
b) Xét ∆ABG và ∆ACG ta có :
AG chung
BAH = CAH (cmt)
AB = AC (cmt)
=> ∆ABG = ∆ACG (c.g.c)(dpcm)
c) Vì AH = 9cm (gt)
Mà AD = 2/3AH
=> AD = 6cm
=> DH = 9 - 6 = 3 cm
Mà AH là trung tuyến BC
=> BH = HC = BC/2 = 4 cm
Áp dụng định lý Py ta go vào ∆ vuông BHD ta có
=> BD = 5 cm
Bài 2) Áp dụng định lý Py ta go vào ∆ vuông ABC ta có :
BC = 10 cm
b) Xét ∆ vuông ABM và ∆ vuông BMC ta có :
BM chung
ABM = CBM ( BM là phân giác)
=> ∆ABM = ∆BMC ( ch - gn )
c) Vì ∆ABM = ∆BMC (cmt)
=> AM = NM
Xét ∆ vuông APM và ∆ MNC ta có :
AM = NM (cmt)
AMP = NMC ( đối đỉnh)
=> ∆APM = ∆MNC ( cgv - gn )
d) Vì ∆ APM = ∆MNC (cmt)
=> PM = MC
=> ∆MPC cân tại M
Mà K là trung điểm PC
=> MK là trung tuyến đồng thời là trung trực và là phân giác ∆PMC
=> MK vuông góc với PC
=> M; K thẳng hàng
Mà BM là phân giác ABC
=> B ; M thẳng hàng
=> B ; M ; K thẳng hàng
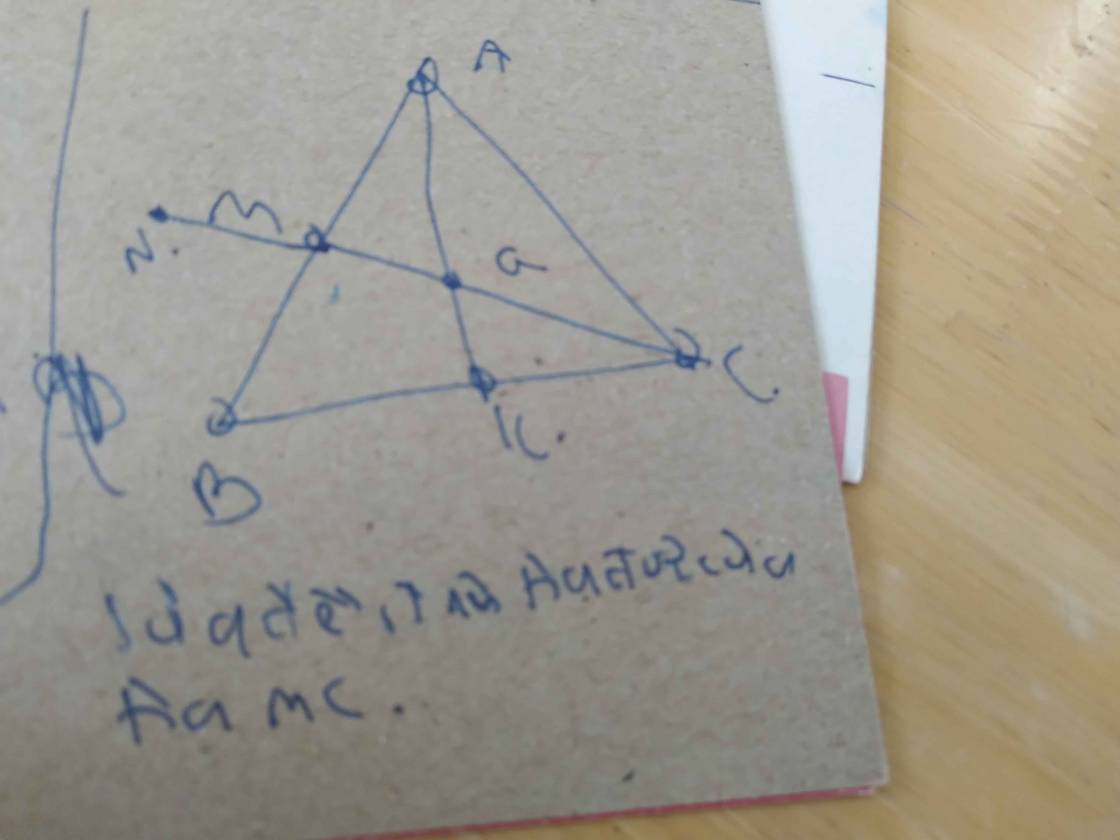

Ta có, tam giác AH là đường cao của tam giác cân ABC => góc AHB=90 độ=> góc BHE=90 độ
Xét tam giác BHG và tam giác BHE, ta có :
BH chung
GH= EH (gt)
góc AHB= góc BHE (=90 độ)
=> Tam giác BHG = Tam giác BHE
=> BG =BH ( cặp cạnh tương ứng )
=> Ta cần có GE = BG = BH thì tam giác BBE cân
bạn ơi vẽ hình nha để mìh giải gíup bạn nhanh hơn