Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

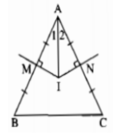
Gọi M, N là trung điểm của AB và AC.
Ta có: AM = 1/2 AB (gt); AN = 1/2 AC (gt)
Mà AB = AC (gt)
⇒ AM = AN
Xét hai tam giác vuông AMI và ANI, ta có:
∠(AMI) = ∠(ANI) = 90o
AM = AN (chứng minh trên)
AI cạnh huyền chung
⇒ ΔAMI= ΔANI (cạnh huyền, cạnh góc vuông)
⇒ ∠(A1) = ∠(A2) (hai góc tương ứng)
Vậy AI là tia phân giác của ∠(BAC)

A B C M N I 1 2
Gọi M, N là trung điểm của AB, AC
Xét hai tam giác vuông AMI và ANI có:
AI: cạnh huyền chung
AM = AN (gt)
Vậy: \(\Delta AMI=\Delta ANI\left(ch-cgv\right)\)
Suy ra: \(\widehat{A_1}=\widehat{A_2}\) (hai góc tương ứng)
Do đó: AI là tia phân giác của góc A.

trong tam gaic can giao diem cua cac duong trung truc la gai diem cua cac duong phan giac
xong!
gọi k lag trung điểm của AB , H là trung Ac
Xét t/g KAI vs HAI
có K = H = 90 độ
KA = HA
chung AI
=> 2 t/g =nhau ( ch -cgv)
A1= A2 => AI là phân giác ( dễ cực lun )

mình làm theo cách của HKII nhé
xét tam giác ABC có
các đường trung trực của AB, AC cắt nhau tại I (gt)
=> I là gđ của 3 đường trung trực trong tam giác ABC
=> AI là đường trung trực của BC
mà tam giác ABC cân tại A (gt)
nên AI là đường phân giác của tam giác ABC
=> AI là tia phân giác của góc A

1.Vì các tia phân giác của các góc B và C cắt nhau tại I
\(\Rightarrow\)I là giao của các đường phân giác trong tam giác
\(\Rightarrow\)AI là tia phân giác của góc A
1.
Kẻ: \(ID\perp AB;IE\perp BC;IF\perp AC\)
\(\widehat{IDB}=\widehat{IEB}=90^0\)
\(\widehat{DBI}=\widehat{EIB}\left(gt\right)\)
BI cạnh huyền chung
⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\widehat{IEC}=\widehat{IFC}=90^0\)
\(\widehat{ECI}=\widehat{FCI}\left(gt\right)\)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
\(\widehat{IDA}=\widehat{IFA}=90^0\)
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra\(\widehat{DAI}=\widehat{FAI}\) (hai góc tương ứng)
Vậy AI là tia phân giác của \(\widehat{A}\)