Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAKM vuông tại K và ΔANM vuông tại N có
AM chung
góc KAM=góc NAM
=>ΔAKM=ΔANM
=>MK=MN
b: BM=CM=3cm
AM=căn 5^2-3^2=4cm
c; AK=AN
MK=MN
=>AM là trung trực của KN
=>AM vuông góc KN

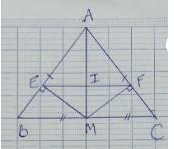
a) Xét ΔABM và ΔACM có:
AB = AC (ΔABC cân tại A)
Cạnh AM chung
BM = CM (AM là đường trung tuyến của BC)
⇒ ΔABM = ΔACM (c.c.c)
Vậy ΔABM = ΔACM

a: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
b: Xét ΔHME vuông tại H và ΔKMF vuông tại K có
MH=MK
\(\widehat{HME}=\widehat{KMF}\)
Do đó; ΔHME=ΔKMF
Suy ra: HE=KF
mà AH=AK
nên AE=AF
hay ΔAEF cân tại A

A B C M H K G
A) XÉT \(\Delta ABC\)VUÔNG TẠI
CÓ AM LÀ TRUNG TUYẾN \(\Rightarrow AM=\frac{1}{2}BC\Leftrightarrow AM=BM=CM\)
XÉT TAM GIÁC AMC CÓ AM=CM => TAM GIÁC AMC CÂN TẠI M
MÀ TRONG TAM GIÁC CÂN ĐƯỜNG CAO CŨNG LÀ TIA PHÂN GIÁC => MH LÀ PHÂN GIÁC CỦA \(\widehat{AMC}\)
\(\Rightarrow\widehat{AMH}=\widehat{HMC}\)
XÉT \(\Delta AMH\)VÀ \(\Delta CMH\)CÓ
\(AM=MC\left(CMT\right)\)
\(\widehat{AMH}=\widehat{HMC}\left(CMT\right)\)
MH LÀ CẠNH CHUNG
=>\(\Delta AMH\)=\(\Delta CMH\)(C-G-C)
=> AH= CH ( HAI CẠNH TƯƠNG ỨNG)
=> BH LÀ ĐƯỜNG TRUNG TUYẾN CỦA TAM GIÁC ABC
VÌ HAI TĐƯỜNG TRUNG TUYẾN AM VÀ BH CẮT NHAU TẠI G
=> G LÀ TRỌNG TÂM CỦA TAM GIÁC ABC
B)
XÉT \(\Delta ABC\)VUÔNG TẠI A
CÓ AM LÀ TRUNG TUYẾN
\(\Rightarrow AM=\frac{1}{2}BC\left(Đ/L\right)\)P/S CHỈ ÁP DỤNG TRAM GIÁC GIÁC VUÔNG
c) Tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông, bạn lên mạng tham khảo , EZ
a) AM = MC nên tam giác AMC cân tại M nên MH là đường cao cũng là trung tuyến hay H là trung điểm của AC nên BH là trung tuyến của tam giác ABC
Mà AM cũng là trung tuyến của tam giác ABC nên G trọng tâm của tam giác ABC

a, Xét tam giác ABM và tam giác ACM có
AB=AC(gt)
BM=CM(gt)
^ABC=^ACB(gt)
=> tam giác ABM= tam giác ACM(c-g-c)
=> ^AMB=^AMC(2 g tương ứng)
=> ^AMB=^AMC=180 độ /2 =90 độ
hay AM vuông góc vs BC
b, Ta có: BM=MC=1/2 BC=5
Áp dụng đly pitago vào tam giác vuông ABM có:
AM^2=AB^2-BM^2=13^2-5^2=144
=> AM=12