Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M N 1 2 2 1 E F 1 1 2 2 O
CM : a) Ta có: t/giác ABC cân tại A
=> góc B2 = góc C2
Mà góc B1 + góc B2 = 1800
góc C1 + góc C2 = 1800
=> góc B1 = góc C1
Xét t/giác AMB và t/giác ANC
có AB = AC (gt)
góc B1 = góc C1 (cmt)
MB = NC (gt)
=> t/giác AMB = t/giác ANC (c.g.c)
=> AM = AN (hai cạnh tương ứng)
=> t/giác AMN là t/giác cân tại A
b) Ta có: t/giác AMN cân tại A
=> góc M = góc N
Xét t/giác BME và t/giác CNF
có góc E1 = góc F1 = 900 (gt)
BM = CN (gt)
góc M = góc N (cmt)
=> t/giác BME = t/giác CNF (cạnh huyền - góc nhọn)
c,d) tự làm

Hình tự kẻ nha
a)Xét 2 tam giác vuông ABH và ACH có
Góc AHB = góc AHC (=90°)
AB= AC ( tam giác ABC cân tại A)
Góc ABC = góc ACB (tam giác ABC cân tại A)
=>2 tam giác vuông ABH=ACH (cạnh huyền -góc nhọn)
b)Tam giác ABC cân =>góc ABC=gócACB
=>gócABM=gócACN
Xét 2 tam giác ABM và ACN
AB=AC ( tam giác ABC cân tại A)
Góc ABM=góc ACN (cmt)
BM=CN(gt)
=> tam giác ABM=tam giác ACN
=>AM=AN
Do đó tam giác AMN cân tại A
c) Phần này hình như sai đề
A B C M N H E F K 1 2 1 1 2 3 3 2
a) Xét t/giác ABH và t/giác ACH
có: AB = AC (gt)
\(\widehat{H_1}=\widehat{H_2}=90^0\)(gt)
\(\widehat{B_1}=\widehat{C_1}\) (gt)
=> t/giác ABH = t/giác ACH (ch - gn)
b) Ta có: \(\widehat{B_1}+\widehat{ABM}=180^0\)(kề bù)
\(\widehat{C_1}+\widehat{ACN}=180^0\) (kề bù)
Mà \(\widehat{B_1}=\widehat{C_1}\) (gt) => \(\widehat{ABM}=\widehat{ACN}\)
Xét t/giác ABM và t/giác ACN
có AB = AC (gt)
\(\widehat{ABM}=\widehat{ACN}\) (cmt)
BM = CN (gt)
=> t/giác ABM = t/giác ACN (c.g.c)
=> AM = AN (2 cạnh t/ứng)
=> t/giác AMN cân
c) Ta có: t/giác MEB vuông tại A => \(\widehat{M}+\widehat{B_2}=90^0\)
t/giác FCN vuông tại F => \(\widehat{C_2}+\widehat{N}=90^0\)
Mà \(\widehat{M}=\widehat{N}\)(Vì t/giác AMN cân tại A) => \(\widehat{B_2}=\widehat{C_2}\) (1)
Ta lại có: \(\widehat{B_2}=\widehat{B_3}\) (Đối đỉnh); \(\widehat{C_2}=\widehat{C_3}\)(đối đỉnh) (2)
Từ (1) và (2) => \(\widehat{B_3}=\widehat{C_3}\) => t/giác BKC cân tại K
có KH là đường cao
=> KH cũng là đường trung trực của cạnh BC (t/c của t/giác cân) (3)
(đoạn này chưa học có thể xét t/giác KBH và t/giác KCH => BH = CH => KH là đường trung trực)
t/giác ABH = t/giác ACH (cm câu a) => BH = CH
=> AH là đường trung tuyến
mà AH cũng là đường cao
=> AH là đường trung trực của cạnh BC (4)
Do A \(\ne\)K (5)
Từ (3); (4); (5) => A, H, K thẳng hàng

a, Xét △BAH vuông tại H và △CAH vuông tại H
Có: AH là cạnh chung
AB = AC (gt)
=> △BAH = △CAH (ch-cgv)
=> BH = CH (2 cạnh tương ứng)
Mà H nằm giữa B, C
=> H là trung điểm BC
Ta có: BH + CH = BC => BH + BH = 12 => 2BH = 12 => BH = 6 (cm)
Xét △BAH vuông tại H có: AH2 + BH2 = AB2 (định lý Pytago)
=> AH2 = AB2 - BH2
=> AH2 = 102 - 62
=> AH2 = 64
=> AH = 8 (cm)
b, Ta có: MH = MB + BH và HN = HC + CN
Mà BH = HC (cmt) ; MB = CN (gt)
=> MH = HN
Xét △MHA vuông tại H và △NHA vuông tại H
Có: AH là cạnh chung
MH = HN (cmt)
=> △MHA = △NHA (2cgv)
=> HMA = HNA (2 góc tương ứng)
Xét △AMN có: AMN = ANM (cmt) => △AMN cân tại A
c, Xét △MBE vuông tại E và △NCF vuông tại F
Có: EMB = FNC (cmt)
MB = CN (gt)
=> △MBE = △NCF (ch-gn)
=> MBE = NCF (2 góc tương ứng)
d, Vì △MHA = △NHA (cmt) => MAH = NAH (2 góc tương ứng)
=> AH là phân giác của MAN
Ta có: AE + EM = AM và AF + FN = AN
Mà EM = FN (△MBE = △NCF) ; AM = AN (△AMN cân tại A)
=> AE = AF
Xét △EAK vuông tại E và △FAK vuông tại F
Có: AK là cạnh chung
AE = AF (cmt)
=> △EAK = △FAK (ch-cgv)
=> EAK = FAK (2 góc tương ứng)
=> AK là phân giác EAF => AK là phân giác MAN
Mà AH là phân giác của MAN
=> AK ≡ AH
=> 3 điểm A, H, K thẳng hàng

a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó:ΔABM=ΔACN
b: Xét ΔHMB vuông tại H và ΔKNC vuông tại K có
MB=NC
\(\widehat{M}=\widehat{N}\)
Do đó: ΔHMB=ΔKNC
Suy ra: BH=CK
c: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
BH=CK
Do đó:ΔABH=ΔACK
Suy ra: AH=AK
Xét ΔAMN có AH/AM=AK/AN
nên HK//MN
hay HK//BC
d: Ta có: ΔHBM=ΔKCN
nên \(\widehat{HBM}=\widehat{KCN}\)
=>\(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O

a) △ABC cân ⇒ \(\widehat{ABC}=\widehat{ACB}\) ⇒\(\widehat{ABM}=\widehat{ACN}\)
Xét △ABM và △ACN có:
\(AB=AC\) ( Vì △ABC cân)
\(\widehat{ABM}=\widehat{ACN}\left(cmt\right)\)
BM=CN(gt)
Do đó : △ABC=△ACN\(\left(c.g.c\right)\)
b)Xét △vuoongAHB và △vuoongAKC có
AB=AC(vì △ABC cân)
\(\widehat{HAB}=\widehat{KAC}\) (vì △ABM=△ACN)
⇒△AHB=△AKC ( cạnh huyền góc nhọn)
⇒AH=AK
a, Ta có : ^ABM = ^MBC - ^ABC (1)
^ACN = ^NCB - ^ACB (2)
Từ (1) ; (2) suy ra ^ABM = ^ACN
Xét tam giác ABM và tam giác ANC có :
^ABM = ^ANC ( cmt )
AB = AC ( gt )
MB = NC (gt)
Vậy tam giác ABM = tam giác ACN ( c.g.c )
=> AM = AN ( 2 cạnh tương ứng )
Xét tam giác AMN có : AN = AM
Vậy tam giác AMN là tam giác cân tại A
=> ^M = ^N (3)
b, Ta có : ^AMB = ^ABH ( cùng phụ ^HBM ) (4)
^ACK = ^ANC ( cùng phụ ^KCN ) (5)
Từ (3) ; (4) ; (5) suy ra : ^ABH = ^ACK
=> ^HBM = ^KCN
Xét tam giác AHB và tam giác AKC ta có :
^ABH = ^ACK ( cmt )
AB = AC
^AHB = ^AKC = 900
Vậy tam giác AHB = tam giác AKC ( ch - gn )
=> AH = AK ( 2 cạnh tương ứng )
c, Ta có : ^HBM = ^OBC ( đối đỉnh )
^KCN = ^BCO ( đối đỉnh )
mà ^HBM = ^KCN (cmt)
Xét tam giác OBC có :
^OBC = ^OCB vậy tam giác OBC cân tại O

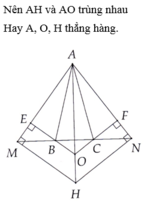
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
b: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó;ΔABM=ΔACN
Suy ra: \(\widehat{M}=\widehat{N}\)
Xét ΔEBM vuông tại E và ΔFCN vuông tại F có
BM=CN
\(\widehat{M}=\widehat{N}\)
Do đó: ΔEBM=ΔFCN
Suy ra: \(\widehat{EBM}=\widehat{FCN}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
=>IB=IC
mà AB=AC
và HB=HC
nên A,H,I thẳng hàng