

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a )
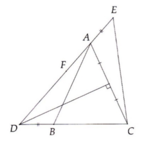
ta có : \(\widehat{C_1}=\widehat{C_2}\) ( 2 góc đối đỉnh )
mà \(\widehat{C_1}=\widehat{B}\) ( tam gíac ABC cân tại A )
Do do : \(\widehat{C_2}=\widehat{B}\)
xét \(\Delta ABDva\Delta ICE,co:\)
AB = AC = IC ( gt )
BD=CE ( gt )
\(\widehat{C_2}=\widehat{B}\) (cmt )
Do do : \(\Delta ABD=\Delta ICE\left(c-g-c\right)\)

Cho tam giác ABC vuông tại A, BD là tia phân giác của góc B ( d thuộc AC). Kẻ DEvuông gócBC ( E thuộc BC). Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh rằng:
a) BD là đường trung trực của AF
b) AD < BC
c) Ba điểm E, D, F thẳng hàng

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau