Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C I N M 1 2 1 2 1 2
Ta có: BI là phân giác \(\widehat{ABC}\Rightarrow\widehat{B_1}=\widehat{B_2}\)
CI là phân giác \(\widehat{ACB}\Rightarrow\widehat{C_1}=\widehat{C_2}\)
\(MN//BC\Rightarrow\widehat{I_1}=\widehat{B_2}\),\(\widehat{I_2}=\widehat{C_2}\)
+) Vì \(\widehat{B_1}=\widehat{B_2}\);\(\widehat{I_1}=\widehat{B_2}\)
\(\Rightarrow\widehat{B_1}=\widehat{I_1}\Rightarrow\Delta MBI\)cân tại M
\(\Rightarrow MB=MI\)
+) Vì \(\widehat{C_1}=\widehat{C_2}\);\(\widehat{I_1}=\widehat{C_2}\)
\(\Rightarrow\widehat{C_1}=\widehat{I_2}\Rightarrow\Delta NCI\)Cân tại N
\(\Rightarrow NC=NI\)
Ta có: \(MN=MI+NI\)
mà \(MB=MI\);\(NC=NI\)
\(\Rightarrow MN=MB+NC\left(đpcm\right)\)

Xét ΔDAI có góc DAI=góc DIA(=góc BAI)
nen ΔDAI cân tại D
=>DA=DI
Xét ΔEIB có góc EIB=góc EBI(=góc ABI)
nên ΔEIB cân tại E
=>EB=EI
DE=DI+IE
=>DE=EB+AD



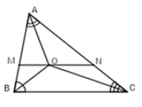


*Có: MI // BC (GT)
\(\Rightarrow\widehat{MIB}=\widehat{IBC}\) (2 góc so le trong) (1)
Mà: \(\widehat{MBI}=\widehat{IBC}\) (BI là phân giác) (2)
Từ (1) và (2) \(\Rightarrow\widehat{MIB}=\widehat{MBI}\)
=> ΔMBI cân tại M
=> MI = MB (5)
*Có NI // BC (GT)
\(\Rightarrow\widehat{NIC}=\widehat{ICB}\) (2 góc so le trong) (3)
Mà: \(\widehat{NCI}=\widehat{ICB}\) (CI là phân giác) (4)
Từ (3) và (4) \(\Rightarrow\widehat{NIC}=\widehat{NCI}\)
=> ΔNCI cân tại N
=> NI = NC (6)
Từ (5) và (6) => MI + NI = MB + NC
Mà: MI + NI = MN
=> MN = MB + NC
Hay: MN = BM + CN
https://olm.vn/hoi-dap/tim-kiem?q=Cho+tam+gi%C3%A1c+ABC+,+c%C3%A1c+tia+ph%C3%A2n+gi%C3%A1c+c%E1%BB%A7a+g%C3%B3c+B+v%C3%A0+C+c%E1%BA%AFt+nhau+%E1%BB%9F+I+.+Qua+I+k%E1%BA%BB+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+song+song+BC+c%E1%BA%AFt+AB+%E1%BB%9F+D+,+c%E1%BA%AFt+AC+%E1%BB%9F+E+Ch%E1%BB%A9ng+minh+:DE=BD+CE&id=837769
Tham khảo bài này ạ,nó gần giống với bài của cậu,chỉ khác điểm M và N thôi