Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

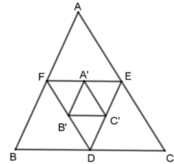
Vì D, E, F theo thứ tự làm trung điểm của BC, CA, AB nên EF, ED, FD là các đường trung bình của tam giác ABC nên E F B C = F D A C = E D A B = 1 2 suy ra ΔABC ~ ΔDEF (c - c - c) theo tỉ số đồng dạng k = 2.
Tương tự ta có A’B’, B’C’, C’A’ là các đường trung bình của tam giác DEF nên ΔA’B’C’ đồng dạng ΔDEF theo tỉ số k = 1 2
Theo tính chất đường trung bình B ' C E F = 1 2 mà E F B C = 1 2 (cmt) suy ra B ' C ' B C = 1 4
Tương tự A ' B ' A B = A ' C ' A C = 1 4
Do đó ΔA’B’C’ đồng dạng ΔABC theo tỉ số k = 1 4
Đáp án: C

Triangle poly1: Polygon A, B, C Segment c: Segment [A, B] of Triangle poly1 Segment a: Segment [B, C] of Triangle poly1 Segment b: Segment [C, A] of Triangle poly1 Segment j: Segment [A, G] Segment k: Segment [B, H] Segment l: Segment [I, C] Segment n: Segment [H, G] Segment q: Segment [O, I] Segment r: Segment [O, G] Segment f_1: Segment [A, D] Segment g_1: Segment [O, K] Segment m: Segment [A, H] Segment p: Segment [B, G] Segment s: Segment [E, D] Segment h_1: Segment [H, O] A = (6.37, 4.19) A = (6.37, 4.19) A = (6.37, 4.19) B = (3.15, -2.53) B = (3.15, -2.53) B = (3.15, -2.53) C = (15.4, -3.36) C = (15.4, -3.36) C = (15.4, -3.36) Point F: Midpoint of c Point F: Midpoint of c Point F: Midpoint of c Point D: Midpoint of a Point D: Midpoint of a Point D: Midpoint of a Point E: Midpoint of b Point E: Midpoint of b Point E: Midpoint of b O = (10.6, -2.67) O = (10.6, -2.67) O = (10.6, -2.67) Point I: Intersection point of f, i Point I: Intersection point of f, i Point I: Intersection point of f, i Point G: Intersection point of d, g Point G: Intersection point of d, g Point G: Intersection point of d, g Point H: Intersection point of e, h Point H: Intersection point of e, h Point H: Intersection point of e, h Point K: Intersection point of j, k Point K: Intersection point of j, k Point K: Intersection point of j, k Point J: Intersection point of f_1, g_1 Point J: Intersection point of f_1, g_1 Point J: Intersection point of f_1, g_1
a) DE là đường trung bình tam giác ABC=>DE//AB và DE=\(\frac{1}{2}\)AB
DE là đường trung bình tam giác OGH=>DE//GH và DE=\(\frac{1}{2}\)GH
=> AB//GH và AB=GH => AHGB là hình bình hành => AG và BH cắt nhau tại trung điểm mỗi đường
CM tương tự: AIGC là hình bình bình hành => AG,IC cắt nhau tại trung điểm mỗi đường
IBCH là hình bình hành => IC,BH cắt nhau tại trung điểm mỗi đường
=> AG,BH,CI đồng quy.
b) K trung điểm AG => OK là trung tuyến tam giác AGO
Mà AD là trung tuyến tam giác AGO ( DG=DO do đối xứng tâm )
=> Giao điểm J của hai đường là trọng tâm tam giác AGO
=> JD =\(\frac{1}{3}\)AD
Mà AD là trung tuyến tam giác ABC
=> J là trọng tâm tam giác ABC
Vậy OK luôn đi qua điểm cố định là trọng tâm tam giác ABC.

a) ΔABC có FB=FC ( gt)
EA=EC ( gt)
Suy ra FE là đường trung bình của ΔABC
b) Ta có: FE=1/2 AB và FE//AB ( FE là đường trung bình của ΔABC)
mà AD cũng =1/2 AB. suy ra FE=AD (1)
có AD∈AB mà FE//AB. suy ra FE//AD (2)
Từ (1) và (2) ➜ DAEF là hình bình hành
Bạn tự vẽ hình nha, sorry vì mình biet nhiu đó

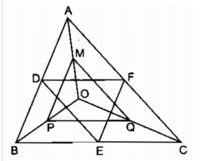
Theo giả thiết D, E, F lần lượt là trung điểm các cạnh AB, BC và CA nên DE, EF, FD là các đường trung bình của tam giác ABC. Do đó, ta có:
DE = 1/2 AC,EF = 1/2 AB,FD = 1/2 BC (1)
Mặt khác, M là trung điểm của OA, P là trung điểm của OB, Q là trung điểm của OC, xét các tam giác OAB, OBC, OCA, ta cũng có:
MP = 1/2 AB,PQ = 1/2 BC, QM = 1/2 AC. (2)
Từ đẳng thức (1) và (2), ta suy ra :
DE = QM, EF = MP, FD = PQ.
Do đó ta có: 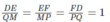
Vậy △ DEF đồng dạng △ QMP theo tỉ số đồng dạng k = 1, trong đó D, E, F lần lượt tương ứng với các đỉnh Q, M, P.