Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi a, b, c, h là độ dài hai cạnh góc vuông, cạnh huyền và đường cao
Có \(c=\sqrt{a^2+b^2},ab=ch\Leftrightarrow h=\dfrac{ab}{c}\)
Có \(\left\{{}\begin{matrix}a+b=70\\c+h=74\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a+b=70\\\sqrt{a^2+b^2}+\dfrac{ab}{\sqrt{a^2+b^2}}=74\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}a+b=70\\a^2+b^2+ab=74\sqrt{a^2+b^2}\end{matrix}\right.\)
PT dưới tương đương: \(\left(a+b\right)^2-ab=74\sqrt{\left(a+b\right)^2-2ab}\)
\(\Leftrightarrow ab=1200\)
Suy ra \(\left\{{}\begin{matrix}a+b=70\\ab=1200\end{matrix}\right.\), a và b là hai nghiệm của pt \(x^2-70x+1200=0\)
\(\Leftrightarrow a=30,b=40\)
Vậy độ dài các cạnh góc vuông, cạnh huyền và đường cao là 30, 40, 50, 24.

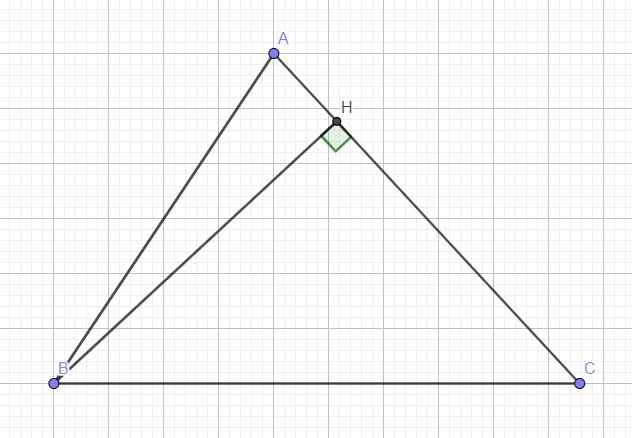
Kẻ đường cao BH (H thuộc AC)
Do góc A nhọn \(\Rightarrow\) H nằm giữa A và C
Ta có: \(S_{ABC}=\dfrac{1}{2}BH.AC\Leftrightarrow\dfrac{2}{5}bc=\dfrac{1}{2}BH.b\)
\(\Rightarrow BH=\dfrac{4c}{5}\)
Áp dụng Pitago cho tam giác vuông ABH:
\(AH^2=AB^2-BH^2=c^2-\left(\dfrac{4c}{5}\right)^2=\dfrac{9c^2}{25}\Rightarrow AH=\dfrac{3c}{5}\)
\(\Rightarrow CH=AC-AH=b-\dfrac{3c}{5}\)
Pitago tam giác vuông BCH:
\(BC=\sqrt{BH^2+CH^2}=\sqrt{\left(\dfrac{4c}{5}\right)^2+\left(b-\dfrac{3c}{5}\right)^2}=\sqrt{b^2-\dfrac{6}{5}bc+c^2}\)

A B C
Gỉa sử \(\Delta ABC\) có \(AB=3AC;\widehat{A}=90^0\)
Khi đó \(S\Delta ABC=\frac{1}{2}.AB.AC=\frac{1}{2}.AB.\frac{1}{3}.AB=24\Rightarrow AB^2=144\Rightarrow AB=12\left(cm\right)\)
\(\Rightarrow AC=4\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+4^2}=4\sqrt{10}\left(cm\right)\)
Gọi cạnh góc vuông nhỏ là x (cm,x>0)
=> cạnh góc vuông lớn là 3x(cm)
Diện tích là 24 \(cm^2\)nên ta có : \(\frac{3x.x}{2}\)= 24 => x=4 (TMĐK)
=> cạnh góc vuông lớn là 12cm
Vậy số đo cạnh huyền là \(4\sqrt{10}\)cm

1) ta có góc BAF+góc DAE=90 ĐỘ
góc DAK +góc DAE=90 ĐỘ
=> góc BAF= góc DAK
XÉT 2 TAM GIÁC TRÊN THEO TRƯỜNG HỢP G.C.G
=>tam giác ABF=tam giác DAK
==>AK=AF => tam giác AKF cân tại A
2)XÉT TAM GIÁC VUÔNG KCF CÓ I LÀ TRUNG ĐIỂM CỦA CẠNH HUYỀN KF nên A,F,K thuộc đường tròn đường kính KF (1)
TƯƠNG TỰ VỚI TAM GIÁC VUÔNG AKF ==> A,K,F cùng thuộc đường tròn đường kính KF (2)
TỪ (1) và (2) ==> điều cần chứng minh
3)vì tam giác AKF cân tại A ==> AI là trung tuyến đồng thời là đường cao
==> AI vuông góc với KF
DO ĐÓ góc AIF=90 độ
tương tự câu 2 xét vào 2 tam giác vuông AIF và ABF ==>điều cần chứng minh
đợi một tí thí nữa mk giải típ mệt quá
Ta có \(b=AC=20\)
\(\sin\widehat{B}=\dfrac{AC}{BC}=\sin48^0\approx0,7\Leftrightarrow a=BC=\dfrac{20}{0,7}\approx28,6\)