Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M 1 2 1 2
1.Xét tam giác AMB và tam giác AMC có:
\(AB=AC\);\(AM:\) (cạnh chung)
Do đó \(\Delta AMB=\Delta AMC\)(cạnh huyền-cạnh góc vuông)
2. \(\Delta AMB=\Delta AMC\Rightarrow\widehat{A_1}=\widehat{A_2}\) (hai góc tương ứng)
Suy ra AM là tia phân giác của góc A
3. Chứng minh tương tự.

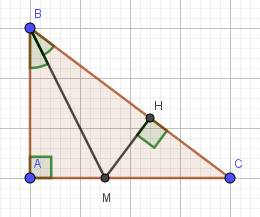
a) Xét hai tam giác vuông: \(\Delta AMB\) và \(\Delta HMB\) có:
BM là cạnh chung
\(\widehat{ABM}=\widehat{HBM}\) (do BM là phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta AMB=\Delta HMB\) (cạnh huyền-góc nhọn)
b) Do \(\Delta AMB=\Delta HMB\) (cmt)
\(\Rightarrow AM=HM\) (hai cạnh tương ứng)
c) \(\Delta MHC\) vuông tại H
\(\Rightarrow MC\) là cạnh huyền nên là cạnh lớn nhất
\(\Rightarrow HM< MC\)
Lại có HM = AM (cmt)
\(\Rightarrow AM< MC\)

nhớ tk cho ming nha
A C B M H N
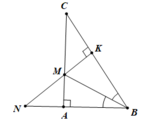
1, Xét tam giác ABC có :
\(BC^2=AC^2+AB^2\)
\(\Leftrightarrow BC^2=4^2+3^2\)
\(\Leftrightarrow BC^2=25\)
\(\Leftrightarrow BC=5\left(cm\right)\)
2,Ta có :\(\widehat{BMA}+\widehat{MBA}=90^O\)
\(\widehat{BMH}+\widehat{MBH}=90^O\)
MÀ \(\widehat{ABM}=\widehat{HBM}\)
Nên \(\widehat{BMA}=\widehat{BMH}\)
Xét tam giác ABM và tam giác HBM có :
\(\widehat{ABM}=\widehat{HBM}\left(gt\right)\)
\(BMchung\)
\(\widehat{BMA}=\widehat{BMH}\)
\(\Rightarrow\Delta BAM=\Delta BHM\left(c.g.c\right)\)
3,Vì \(\Delta BAM=\Delta BHM\Rightarrow AM=MH\left(1\right)\)
Xét \(\Delta HMC\)có :
\(\widehat{MHC}=90^0\)
Suy ra :MC>MH(2)
Từ (1) và(2):AM<MC
4,Ta có :\(\widehat{AMH}+\widehat{HMC}=180^0\left(1\right)\)
Xét tam giác NMA và tam giác CMH có:
\(HC=NA\)
\(\widehat{NAM}=\widehat{CHM}\)
\(MA=MH\left(\Delta BAM=\Delta BHM\right)\)
\(\Rightarrow\Delta NMA=\Delta CMH\left(c.g.c\right)\)
\(\Rightarrow\widehat{NMA}=\widehat{CMH}\)(2)
Từ (1) và(2) : => N,M,H thẳng hàng

c. Do tam giác MKC vuông tại K nên MK < MC (0.5 điểm)
Mà MA = MK ⇒ MA < MC (0.5 điểm)

A )Ta có tam giác ABC cân tại A
=> ˆABC=ˆACBABC^=ACB^
Và AB = AC
Xét hai tam giác vuông BCK và CBH ta có :
BC chung
ˆKBC=ˆBCHKBC^=BCH^
=>BCK = CBH (cạnh huyền - góc nhọn )
=>BH = CK (đpcm)
B) ta có BCK = CBH
=> ˆHBC=ˆKCBHBC^=KCB^
=> ˆABH=ˆACKABH^=ACK^
=> tam giác OBC cân tại O
=> BO = CO
Xét tam giác ABO và tam giác ACO
AB = AC
BO = CO (cmt)
ˆABH=ˆACKABH^=ACK^
=> ABO=ACO (c-g-c)
=> ˆBAO=ˆCAOBAO^=CAO^
=> AO là phân giác góc ABC (đpcm)
C) ta có
AI là phân giác góc ABC
Mà tam giác ABC cân tại A
=> AI vuông góc với cạnh BC (đpcm)

a) Bạn xét 2 tam giác ABM và tam giác ADM ( c-g-c )
Suy ra BM = DM ( 2 cạnh tương ứng )
b) Xét 2 tam giác AKD và tam giác ACB ( g-c-g )
Suy ra AK = AC ( 2 cạnh tương ứng )
Suy ra tan giác AKC cân tại A
Mấy cái tam giác bằng nhau bạn tự chứng minh
Xét tam giác ABC có
AM là phân giác
BM = MC => AM là trung tuyến
Vậy tam giác ABC cân tại A => AB = AC
bằng nhau theo trường hợp gì vậy bạn