Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

Bài 2:
a: Xét ΔABM có
D là trung điểm của AB
F là trung điểm của AM
Do đó: DF là đường trung bình của ΔABM
Suy ra: DF//BM và \(DF=\dfrac{BM}{2}\)(1)
hay DF//BC
Xét ΔAMC có
E là trung điểm của AC
F là trung điểm của AM
Do đó: EF là đường trung bình của ΔAMC
Suy ra: EF//MC và \(EF=\dfrac{MC}{2}\left(2\right)\)
hay EF//BC
Ta có: DF//BC
FE//BC
mà DF,FE có điểm chung là F
nên D,F,E thẳng hàng
b: Ta có: M là trung điểm của BC
nên MB=MC(3)
Từ (1), (2) và (3) suy ra DF=FE
mà D,F,E thẳng hàng
nên F là trung điểm của DE

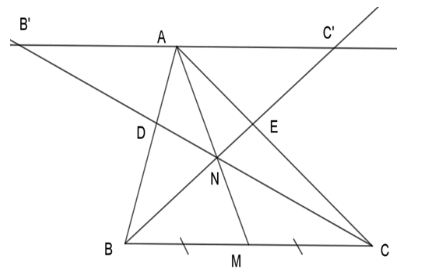
Kẻ đường thẳng đi qua AA song song với BCBC lần lượt cắt CDCD và BEBE kéo dài tại B′B′ và C′C′.
Vì M là trung điểm của BCBC nên BM=MCBM=MC.
Vì AB′//MCAB′//MC, áp dụng định lý Talet ta có:
ANNM=AB′MCANNM=AB′MC (1)
Vì AC′//BMAC′//BM, áp dụng định lý Talet ta có:
ANNM=AC′BMANNM=AC′BM (2)
Từ (1) và (2) ta có: AB′MC=AC′BMAB′MC=AC′BM
Ta có MM là trung điểm của BCBC ⇒⇒BM=MCBM=MC⇒⇒AB′=AC′AB′=AC′ (*)
Vì AB′//BCAB′//BC, áp dụng định lý Talet ta có:
ADDB=AB′BCADDB=AB′BC (**)
Vì AC′//BCAC′//BC, áp dụng định lý Talet ta có:
AEEC=AC′BCAEEC=AC′BC (***)
Từ (*), (**) và (***) ta có:
ADDB=AB′BC=AEEC=AC′BCADDB=AB′BC=AEEC=AC′BC
⇒ADDB=AEEC⇒ADDB=AEEC⇔ADBD=AECE⇔ADBD=AECE hay DE//BC
#vunggoi#